Construct the following angles :
(i) 90∘ (ii) 45∘ (iii) 75∘
To construct the angles 90∘, 45∘, and 75∘, follow these step-by-step instructions:
Step 1: Constructing 90∘
1. Draw a Line Segment: Start by drawing a horizontal line segment BQ.
2. Mark the Midpoint: Identify and mark the midpoint O of the line segment BQ.
3. Draw a Semicircle: Using a compass, place the pointer at point O and draw a semicircle above the line segment BQ.
4. Cut Arcs: With the same compass width, place the pointer at point B and cut an arc on the semicircle. Then, without changing the compass width, place the pointer at point Q and cut another arc on the semicircle.
5. Label the Intersection Points: Let the points where the arcs intersect the semicircle be S and T.
6. Draw the Angle: Draw a line from point O to point S. The angle SOQ formed is 90∘.
Step 2: Constructing 45∘
1. Bisect the 90∘ Angle: To find 45∘, we need to bisect the angle SOQ.
2. Cut Arcs: With the compass pointer at point S, cut an arc above and below the angle. Then, keeping the same width, place the pointer at point O and cut another arc that intersects the previous arcs.
3. Label the Intersection Points: Let the intersection points be A and B.
4. Draw the Angle: Draw a line from point O to point A. The angle AOQ formed is 45∘.
Step 3: Constructing 75∘
1. Construct 60∘: Start by drawing a new line segment AB and marking a midpoint O′.
2. Draw a Semicircle: Draw a semicircle above the line segment AB with the compass centered at O′.
3. Cut Arcs: Cut arcs from points A and B on the semicircle to create points C and D respectively.
4. Construct 60∘: Connect points O′ and C to form angle O′AB which is 60∘.
5. Construct 90∘: Similarly, connect O′ and D to form angle O′AB which is 90∘.
6. Bisect the Angle: To find 75∘, bisect the angle between 60∘ and 90∘.
7. Cut Arcs: Cut arcs from points C and D as before, and label the intersection points E and F.
8. Draw the Angle: Draw a line from point O′ to point E. The angle O′EB formed is 75∘.
Summary of Angles
- The angle SOQ is 90∘.
- The angle AOQ is 45∘.
- The angle O′EB is 75∘.
2. Mark the Midpoint: Identify and mark the midpoint O of the line segment BQ.
3. Draw a Semicircle: Using a compass, place the pointer at point O and draw a semicircle above the line segment BQ.
4. Cut Arcs: With the same compass width, place the pointer at point B and cut an arc on the semicircle. Then, without changing the compass width, place the pointer at point Q and cut another arc on the semicircle.
5. Label the Intersection Points: Let the points where the arcs intersect the semicircle be S and T.
6. Draw the Angle: Draw a line from point O to point S. The angle SOQ formed is 90∘.
2. Cut Arcs: With the compass pointer at point S, cut an arc above and below the angle. Then, keeping the same width, place the pointer at point O and cut another arc that intersects the previous arcs.
3. Label the Intersection Points: Let the intersection points be A and B.
4. Draw the Angle: Draw a line from point O to point A. The angle AOQ formed is 45∘.
2. Draw a Semicircle: Draw a semicircle above the line segment AB with the compass centered at O′.
3. Cut Arcs: Cut arcs from points A and B on the semicircle to create points C and D respectively.
4. Construct 60∘: Connect points O′ and C to form angle O′AB which is 60∘.
5. Construct 90∘: Similarly, connect O′ and D to form angle O′AB which is 90∘.
6. Bisect the Angle: To find 75∘, bisect the angle between 60∘ and 90∘.
7. Cut Arcs: Cut arcs from points C and D as before, and label the intersection points E and F.
8. Draw the Angle: Draw a line from point O′ to point E. The angle O′EB formed is 75∘.
- The angle SOQ is 90∘.
- The angle AOQ is 45∘.
- The angle O′EB is 75∘.
Topper's Solved these Questions
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE
36 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
- HERONS'S FORMULABOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - HERONS'S FORMULAEXERCISE - Revision Exercise
11 Videos
Similar Questions
Construct the following angles :
(i) 45∘ (ii) 135∘
View SolutionConstruct the following angles :
(i) 60∘ (ii) 30∘ (iii) 15∘
View SolutionConstruct the following angles :
(i) 60∘ (ii) 90∘ (iii) 120∘ (iv) 180∘ (v) 270∘
View SolutionConstruct the following angles :
(i) 671∘2 (ii) 221∘2 (iii) 371∘2
View SolutionExpress the following angles in radians.
(i) 120∘ (ii)−600∘
(iii) −144∘
View SolutionExpress the following angles in radians (i) 1, (ii) 20∘ (iii) 135∘
View SolutionWhich trigonometric ratios are positive for the following angles (i) 210∘ (ii) −135∘ (iii) (2π3)c
View SolutionABC is an isosceles right-angled triangle. Assuming AB = BC = x, find the value of each of the following trigonometric ratios :
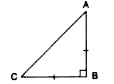
(i) sin45∘
(ii) cos45∘
(iii) tan45∘
View SolutionWrite the complement of each of the following angles: (i) 200 (ii) 350 (iii) 900 (iv) 770 (v) 300
View SolutionConstruct the angles of the following measurements:
(i) 30∘ , (ii)2212∘ , (iii) 15∘
View Solution
