Question

The
diagonals of a parallelogram $ABCD$
intersect
at $O\stackrel{.}{}$
A line
through $O$
meets $AB$
in $xandCD$
in $Y\stackrel{.}{}$
Show that
$ar\left(AXYX\right)=\frac{1}{2}\left(ar{\left|\right|}^{gm}ABCD\right)$

Explanation

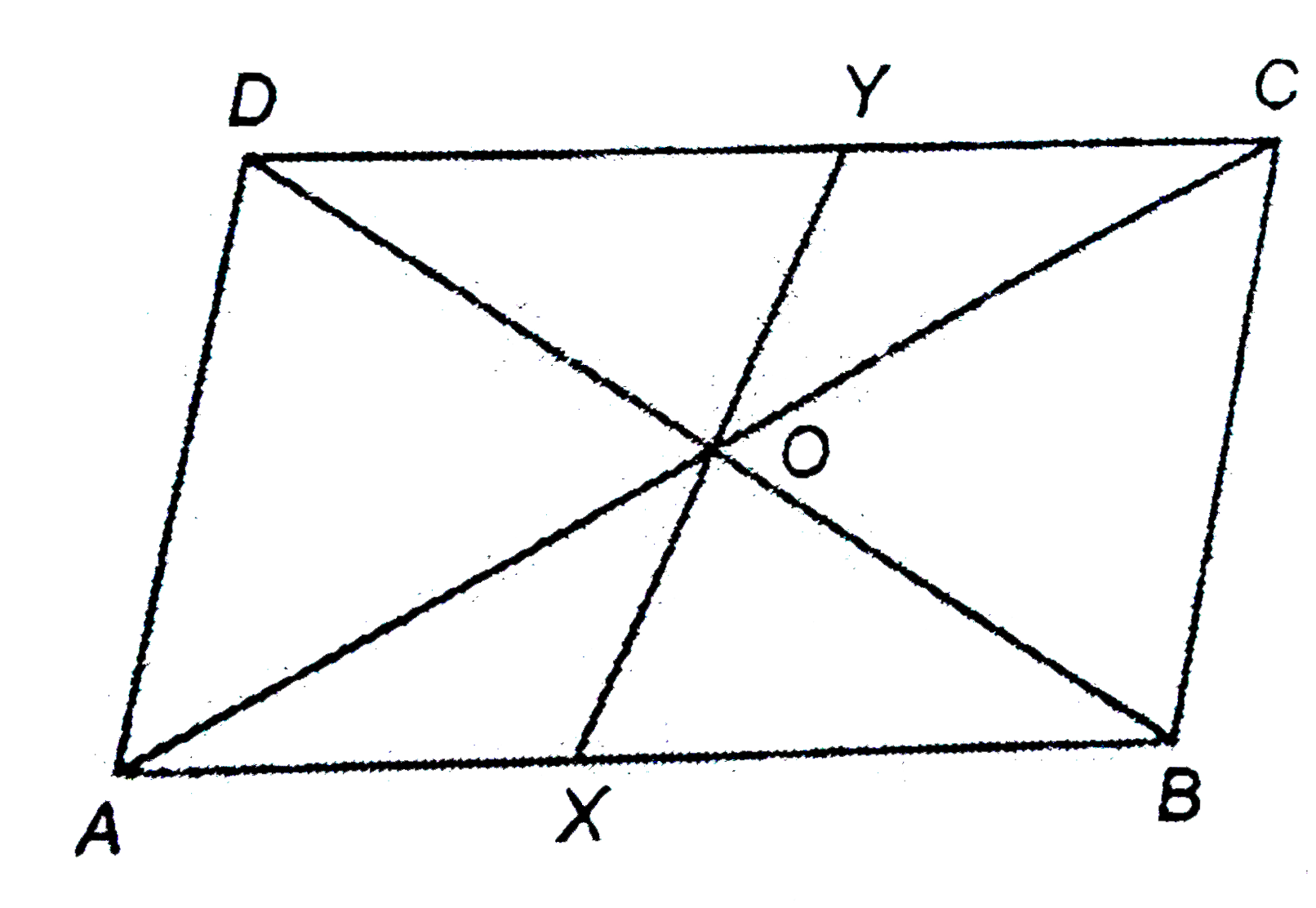
We know that, a diagonal of a parallelogram divides it into two triangles of equal areas.
Now, AC is the diagonal of parallelogram ABCD
`:. " area of "DeltaACD = (1)/(2) xx " are of " square ABCD`...(1)
In `Delta AOX and Delta COY`,
`.:{(AO = CO),(angleAOX = angleCOY),(angleOAX = angleOCY):}`
`:. Delta AOX ~= Delta COY`
`rArr` area of `Delta AOX =` area of `DeltaCOY`
Now, area of `Delta ACD =` are of `squareAOYD + " area of " Delta OCY`
`- " area of " squareAOYD + " area of " Delta AOX` [from (2)]
= area of `squareAXYD`
`:.` From (1), we get
area of `square AXYD = (1)/(2) xx " area of " square ABCD`