In parallelogram ABCD, P is a point on side AB and Q is a ponit on side BC.
Prove that :
(i) ΔCPD and ΔAQD are equal in area.
(ii) Area (ΔAQD)
=Area(ΔAPD)+Area(ΔCPB)
Step by step video & image solution for In parallelogram ABCD, P is a point on side AB and Q is a ponit on side BC. Prove that : (i) DeltaCPD and DeltaAQD are equal in area. (ii) Area (DeltaAQD) = "Area" (DeltaAPD)+ "Area" (DeltaCPB) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (short Answer Questions)
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar
12 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
In a parallelogram ABCD, P is a point on side AD such that 3AP = AD and Q is a point on BC such that 3CQ = BC. Prove that : AQCP is a parallelogram.
View SolutionIn trapezium ABCD, side AB is parallel to side DC. Diagonals AC and BD intersect at point P. Prove that triangles APD and BPC are equal in area.
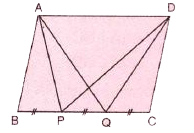
View SolutionIn parallelogram ABCD, points P and Q lie on side BC and trisect it. Prove that :
ar.(ΔAPQ)=ar.(ΔDPQ)
=16×ar. (Parallelogram ABCD)
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔACD)= area (ΔABE)
View SolutionIn parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B.
Prove that P is equidistant from AB and BC.
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔOBD)= area (ΔOCE)
View SolutionO' is an interior point of a parallelogram ABCD. Prove that :
area of ΔAOB+ area of ΔCOD= area of ΔAOD+ area of ΔBOC
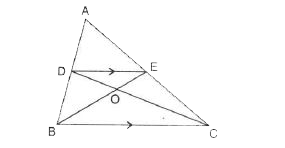
View SolutionIn the following figure, DE is parallel to BC. Show that :
(i) Area(ΔADC)=Area(ΔAEB)
(ii) Area(ΔBOD)=Area(ΔCOE).
View SolutionP is any point inside a parallelogram ABCD. Prove that :
Area (ΔAPB)+Area(ΔCPD)
=Area(ΔAPD)+Area(ΔBPC)
View SolutionIn parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of ΔPOB=40cm2 and OP:OC= 1:2, find :
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
View Solution
