In a quadrilateral ABCD, AM and CN are perpendiculars from the vertices A and C respectively on diagonal BD. Prove that:
area of □ABCD=12×BD×(AM+CN)
Step by step video & image solution for In a quadrilateral ABCD, AM and CN are perpendiculars from the vertices A and C respectively on diagonal BD. Prove that: area of square ABCD = (1)/(2) xx BD xx (AM + CN) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (short Answer Questions)
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar
12 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
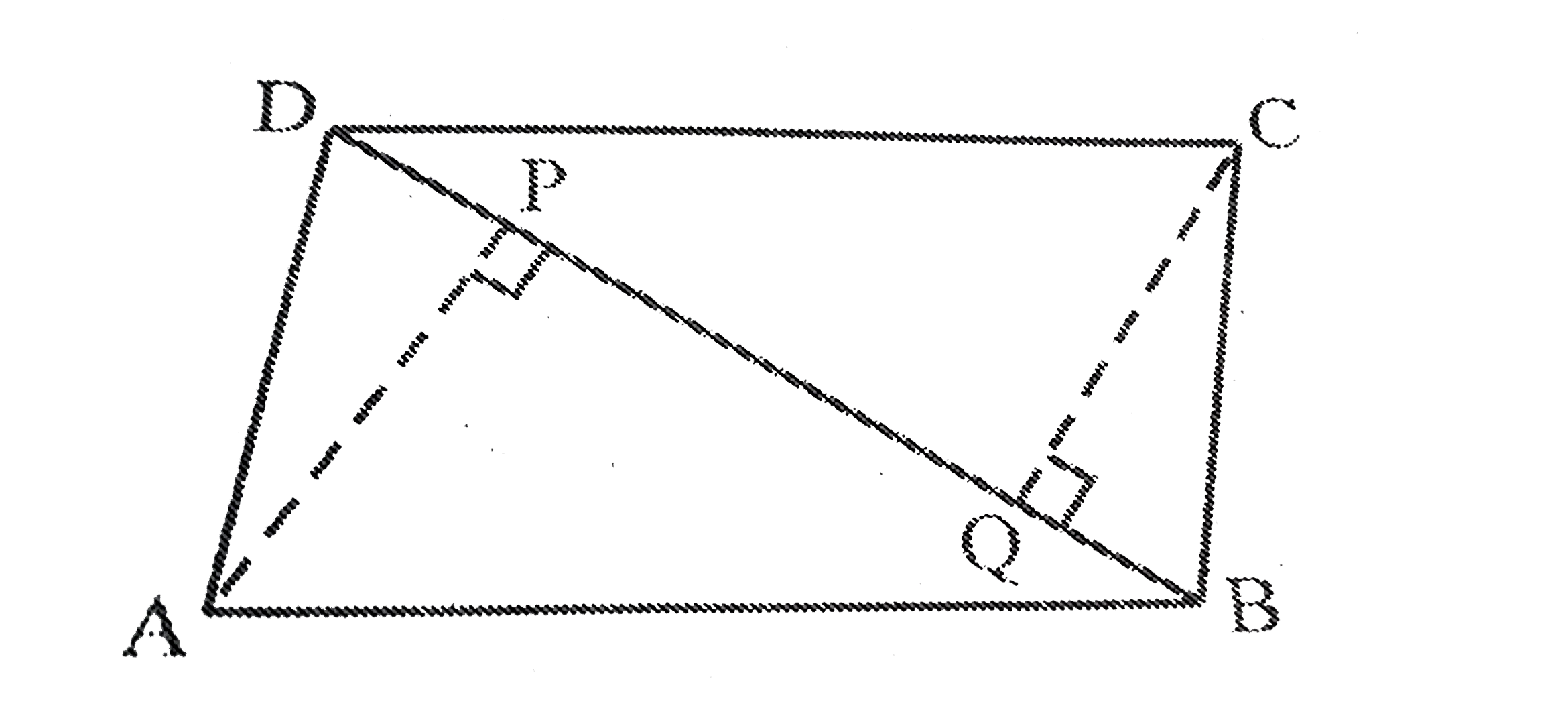
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) ΔAPB≅ ΔCQD
(ii) AP = CQ
View SolutionIn a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC is perpendicular bisector of BD
View SolutionIn a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B)
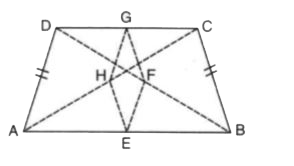
View SolutionABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and AC respectively. Prove that EFGH is a rhombus.
View SolutionM and N are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CN is parallel to AM.
View SolutionIn the quadrilateral ABCD, the diagonals AC and BD are equal and perpendicular to each other. What type of a quadrilateral is ABCD?
View Solution(1, 5) and (-3, -1) are the co-ordinates of vertices A and C respectively of rhombus ABCD. Find the equations of the diagonals AC and BD.
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
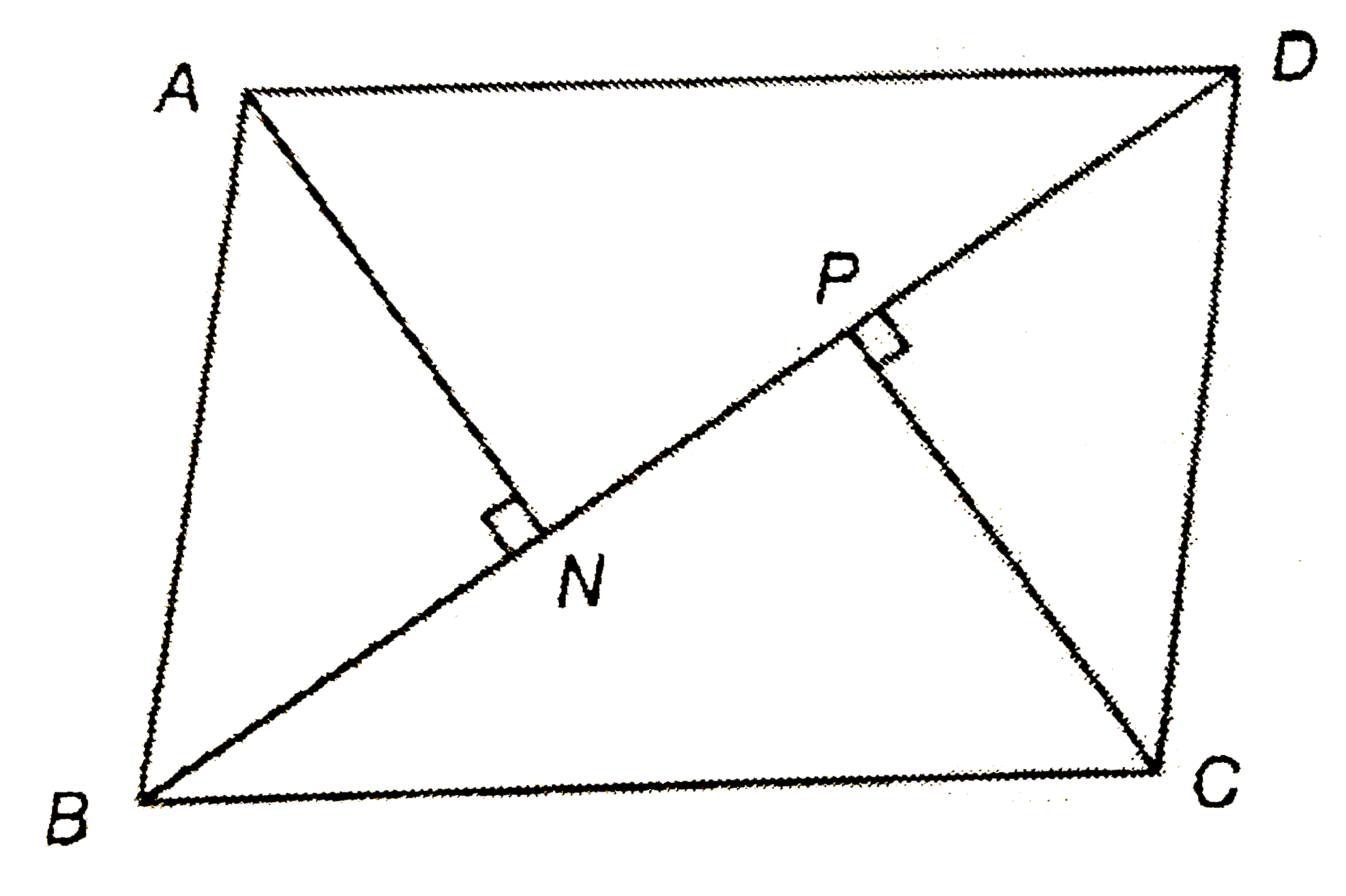
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP.
View Solution
