The largest side of a triangle is twice the smallest side. Its largest side is 3 cm more than the third side. Find the minimum length of the smallest side if the minimum perimeter of the triangle is 62 cm.
To solve the problem step by step, we will define the sides of the triangle based on the information given and then set up an inequality to find the minimum length of the smallest side.
Step 1: Define the sides of the triangle
Let the smallest side of the triangle be x cm. According to the problem:
- The largest side is twice the smallest side, so the largest side is 2x cm.
- The third side is 3 cm less than the largest side, which gives us the third side as 2x−3 cm.
Step 2: Write the inequality for the perimeter
The perimeter of the triangle is the sum of all its sides. According to the problem, the minimum perimeter of the triangle is 62 cm. Therefore, we can write the inequality:
x+2x+(2x−3)≥62
Step 3: Simplify the inequality
Now, let's simplify the left side of the inequality:
x+2x+2x−3=5x−3
So, we have:
5x−3≥62
Step 4: Solve for x
Next, we will solve the inequality for x:
1. Add 3 to both sides:
5x≥62+3
5x≥65
2. Divide both sides by 5:
x≥655
x≥13
Step 5: Conclusion
The minimum length of the smallest side x is 13 cm.
Final Answer
Thus, the minimum length of the smallest side of the triangle is 13 cm.
---
Let the smallest side of the triangle be x cm. According to the problem:
- The largest side is twice the smallest side, so the largest side is 2x cm.
- The third side is 3 cm less than the largest side, which gives us the third side as 2x−3 cm.
The perimeter of the triangle is the sum of all its sides. According to the problem, the minimum perimeter of the triangle is 62 cm. Therefore, we can write the inequality:
x+2x+(2x−3)≥62
Now, let's simplify the left side of the inequality:
x+2x+2x−3=5x−3
So, we have:
5x−3≥62
Next, we will solve the inequality for x:
1. Add 3 to both sides:
5x≥62+3
5x≥65
2. Divide both sides by 5:
x≥655
x≥13
The minimum length of the smallest side x is 13 cm.
Thus, the minimum length of the smallest side of the triangle is 13 cm.
Topper's Solved these Questions
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - EXERCISE
76 Videos
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - NCERT QUESTION
51 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise
30 Videos
- MATHEMATICAL REASONING BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Misellaneous exercise
7 Videos
Similar Questions
The longest side of a triangle is twice the shortest side and the third side is 3 cm longer than the shortest side. If the perimeter of the triangle is at least 39 cm, find the minimum length of the longest side.
View SolutionFind the length of the third side of the triangle.
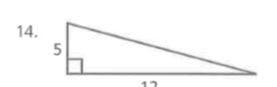
View SolutionFind the length of the third side of the triangle.
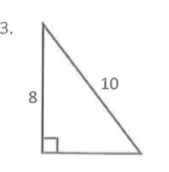
View SolutionThe longest side of a triangle is twice the shortest side and the third side is 2 cm longer than the shortest side. If the perimeter of the triangle is more than 166 cm, then find the minimum length of the shortest side.
View SolutionThe longest side of a triangle is three times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
View SolutionThe longest side of a triangle is three times the shortest side and the third side is 2 cm shorter than the longest side if the perimeter of the triangles at least 61 cm, find the minimum length of the shortest side.
View SolutionThe longest side of a right angled triangle is 4cm longer than one side and 2 cm longer than the other side. Find the longest side.
View SolutionThe longest side of a triangle is twice the shortest side and third side is 3cm longer than shortest side. if perimeter of triangle is more than or equal to 203 cm then minimum length of the shortest side is .
View SolutionThe perimeter of a triangle is 50 cm. One side of the triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
View SolutionFind the perimeter of an equilateral triangle of side 13 cm.
View Solution
