Question

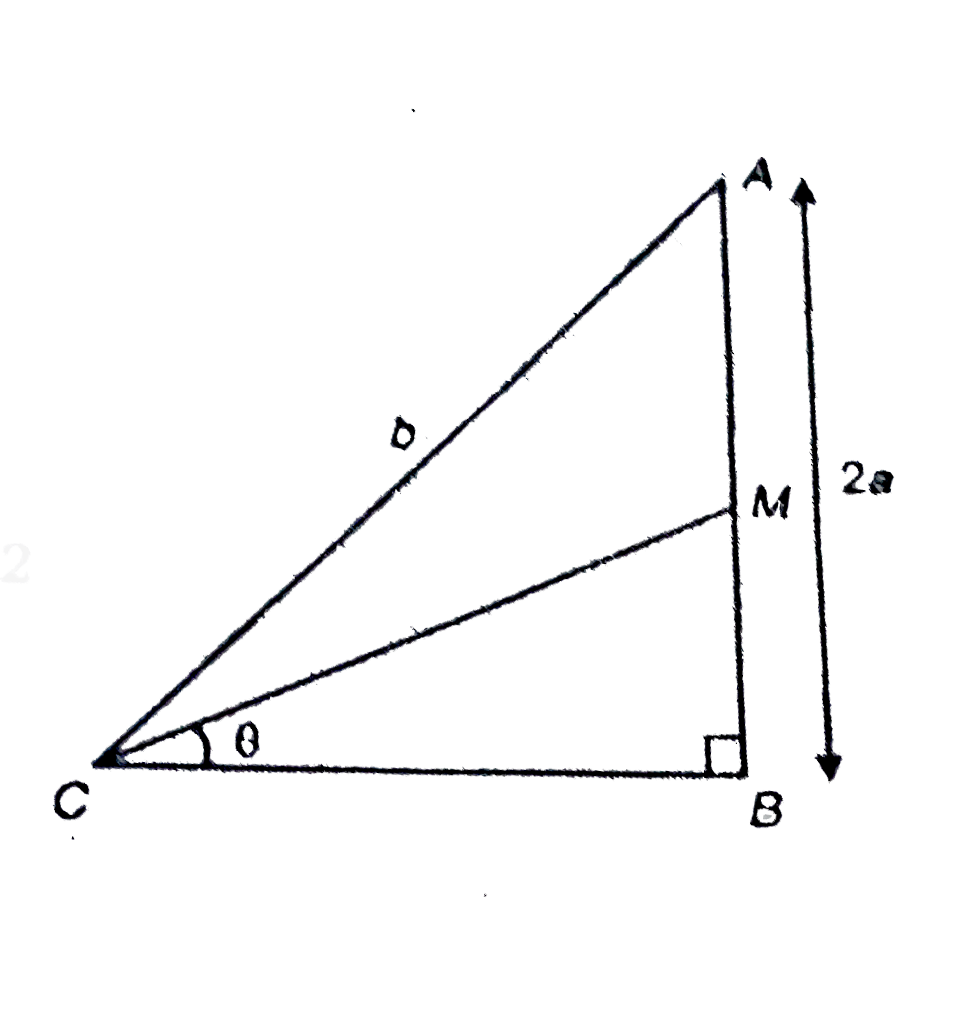
In the adjoining figure , AM =BM and $\angle B={90}^{\circ }.$ If $\angle BCM=\theta$, then find the values of the following :
(i) $\sin \theta$ (ii) $\tan \theta$ (iii) $\sec \theta$

Explanation

From Pythagoras theorem
` BC^(2)=AC^(2)-AB^(2)=b^(2)-(2a)^(2)=b^(2)-4a^(2)`

`rArr BC=sqrt(b^(2)-4a^(2))`
Now , BM` = (AB)/(2)=`
In `DeltaBCM` ,
From Pythagoras theorem
` CM^(2)=BC^(2)+BM^(2)=(b^(2)-4a^(2))+a^(2)=b^(2)-3a^(2)`
`rArr "CM=sqrt(b^(2)-3a^(2))`
(i) ` sintheta=(BM)/(CM)=(a)/(sqrt(b^(2)-3a^(2))`
(ii)` " " tantheta=(BM)/(CM)=(a)/(sqrt(b^(2)-3a^(2))`
(iii)`sectheta=(CM)/(BC)=(sqrt(b^(2)-3a^(2)))/(sqrt(b^(2)-4a^(2))`