In the adjoining frgure ,a right - angled triangle ABC is shown un which AM=CM=3m . If ∠ACM=15∘ , then find AC.
Here , AM=CM
⇒<ACM=<CAM " " (opposite angles of equal sides)
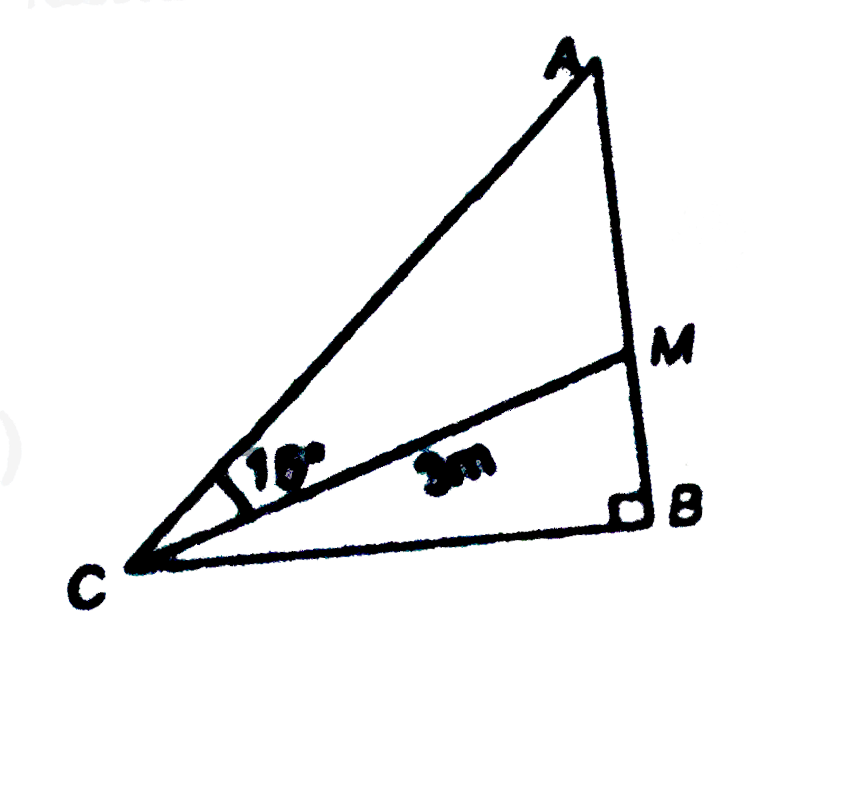
⇒<CAM=15∘
∴<ACB=90∘−15∘=75∘
and <BCM=<ACB−<ACM=75∘−15∘=60∘
In ΔBCM,
cos(<BCM)=BCCM⇒cos60∘=BC3
⇒12=BC3⇒BC=32m
and sin(<BCM)=BMCM⇒sin60∘=BM3
⇒√32=BM3⇒BM=3√32m
∴AB=AM+BM=(3+3√32)m
Now , in ΔABC , from Pythagoras theorem
AC2=AB2+BC2=(3+3√32)2+(32)3=9+274+9√3+94 =18+9√3=9(2+√3)=92(4+2√3)
⇒AC=√9(4+2)√32=3(√3+1)√2m
Topper's Solved these Questions
- INTRODUCTION TO TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Problems From NCERT/exemplar
29 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8a
20 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 11 B
10 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions
8 Videos
Similar Questions
In the adjoining figure , ΔABC is a right - angled triangle , right - angled at B. If ∠A=30∘andAC=8cm, Find (i)BC (ii)AB.

View SolutionConstruct a right-angled triangle ABC in which ∠A=90∘, BC = 6 cm and AB = 4.8 cm.
View SolutionConstruct a right angled ΔABC in which AB=4.2cm,BC=4.5cmand∠B=90∘.
View SolutionConstruct a right angled ΔABC in which BC=5cm,∠B=90∘andAB=4cm.
View SolutionThe following figures shows a right - angled triangle ABC with ∠B=90∘,AB=15 cm and AC = 25 cm. D is a point in side BC and CD = 7 cm. if De ⊥AC, find the length of DE.

View SolutionIn the following figure ABC is a right angled triangle with ∠BAC=90∘,andAD⊥BC.
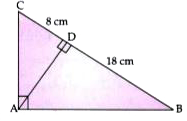
If BD = 18 cm, CD = 8 cm find AD.
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View SolutionIn the given figure, ABC is a right angled triangle with ∠BAC=90∘.

If BD = 18 cm and CD = 8 cm, find AD.
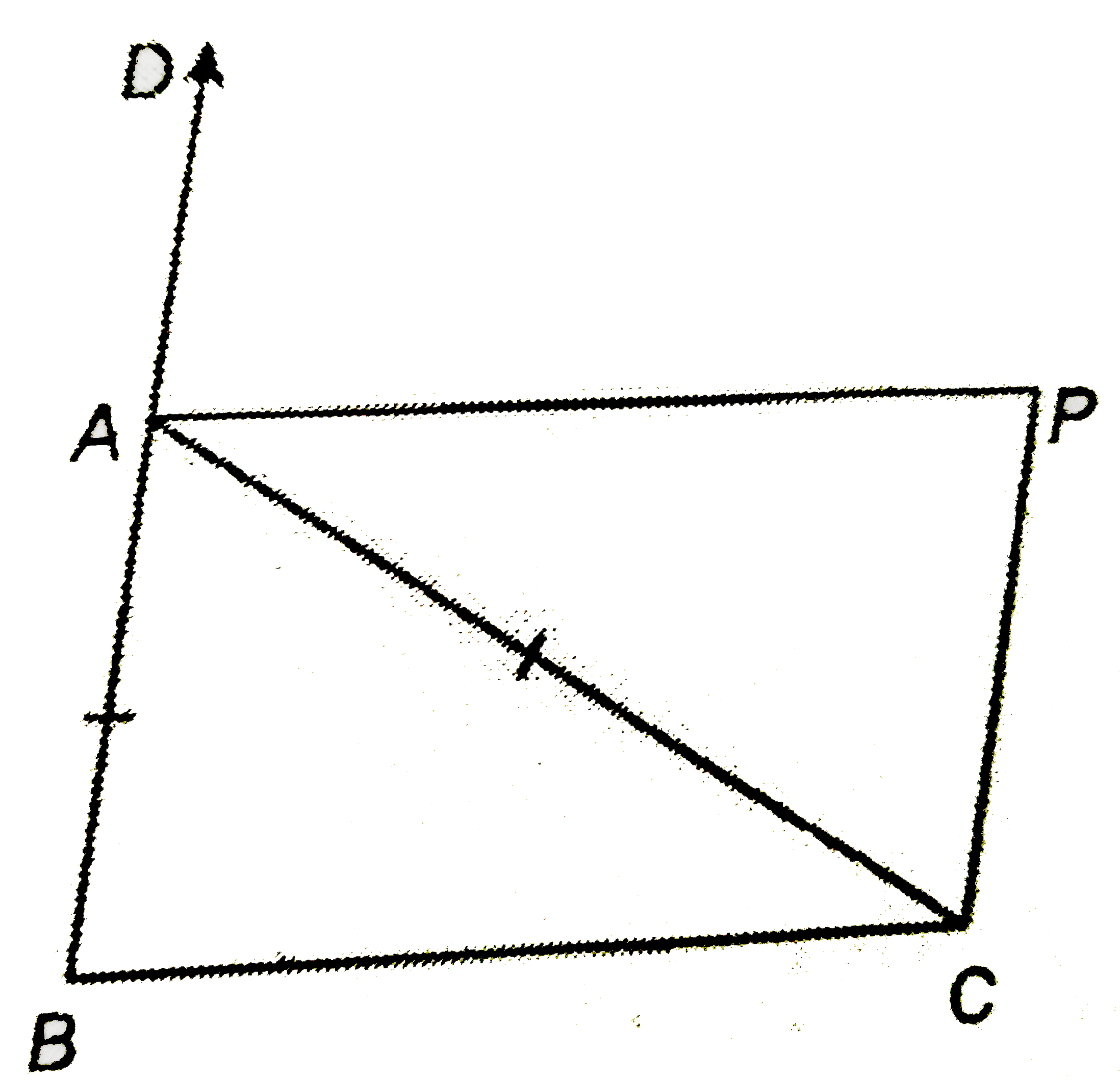
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Δ ABC. Prove that ∠PAC=∠BCAand□ABCP is a parallelogram.
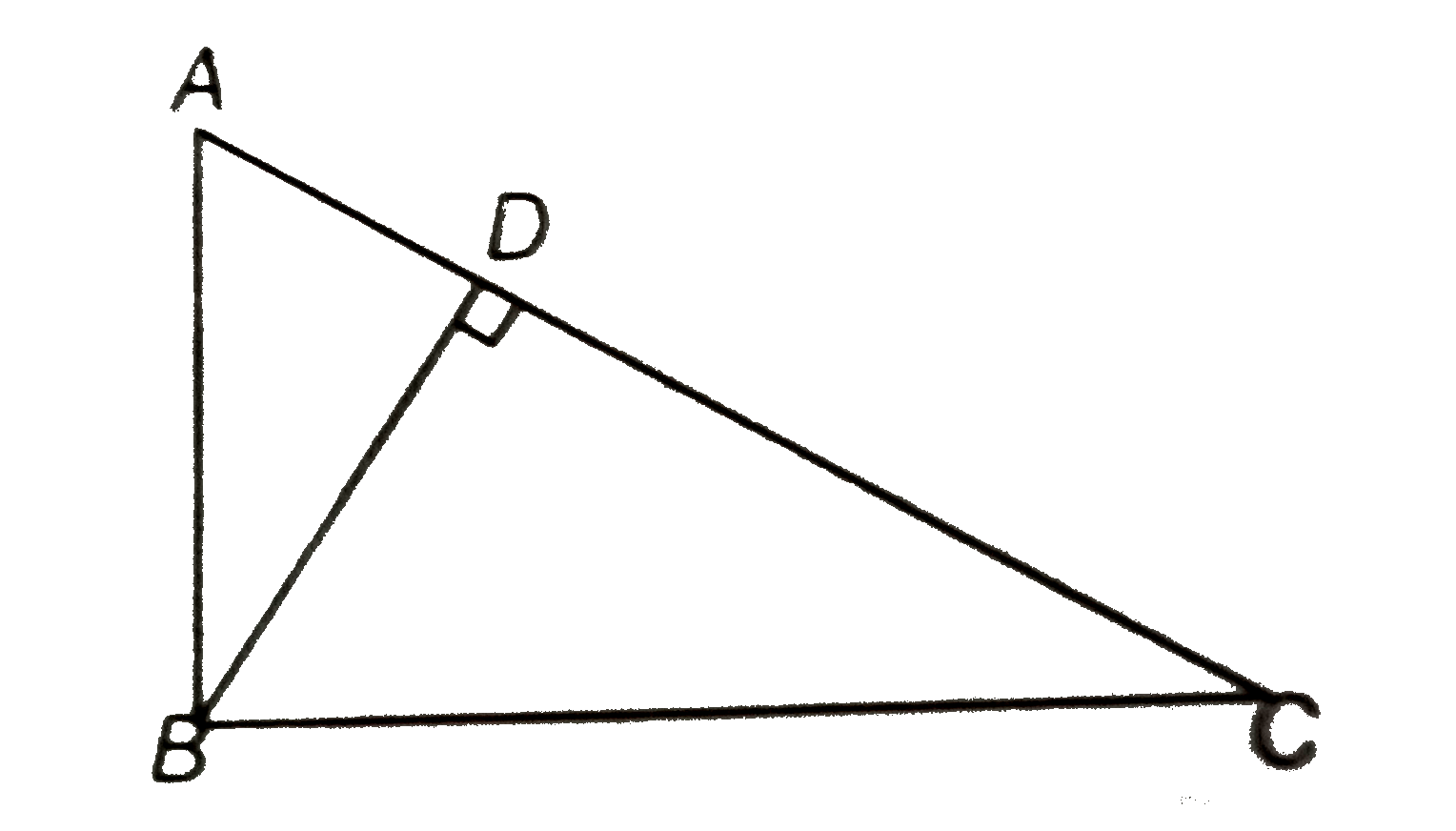
View SolutionIn given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
View Solution
