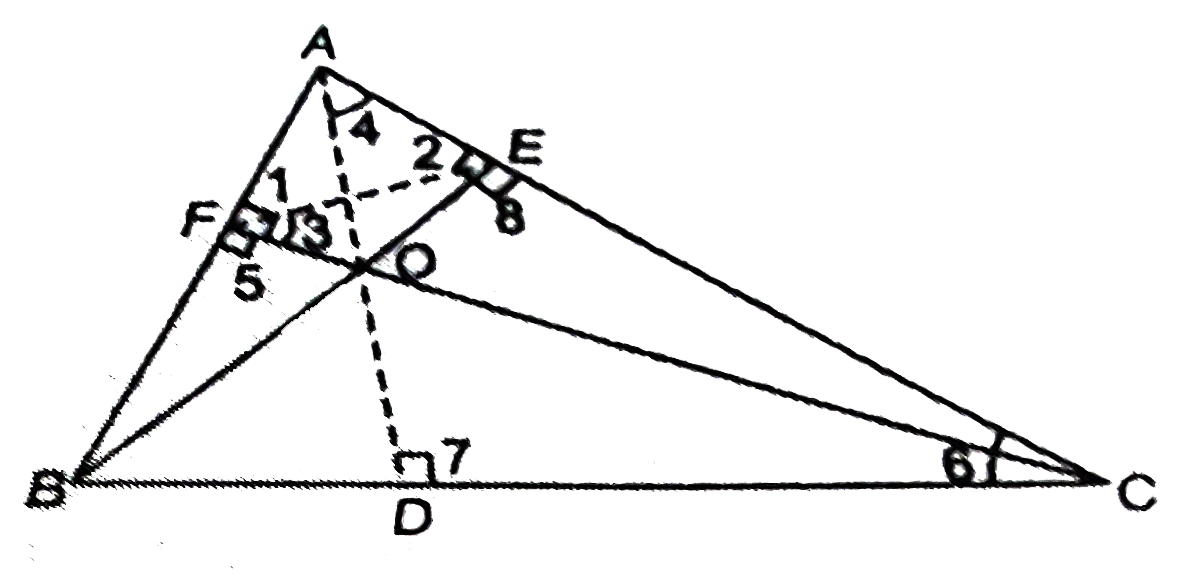
Using vector method, prove that the altitudes of a triangle are concurrent.
Given : ABC be a triangle in which BE and CF are perpendiculars drawn from B and C to the opposite sides AC and AB respectively .
To Prove : All the perpendicualar are concurrent i.e., pass through the same point.
Construction : join AO and produce, where it meets BC at D.
Proof : we have taken BE and CF as perpendiculars intersecting each other at O. if we prove that , it means all the three perpendicualars will pass through O.
Now, (each )
is a cyclic quadrilateral.
(angles of same segment are equal)....(1)
Now, since (each )
But these are the angles subtended by line segmetn joining two points on the same side of the line.
So, B,F,E,C are concyclic.
i.e., square is cyclic.
(sum of opposite angles of a cyclic qluadrilateral)
[form (1)]
Now, in ,
(angle sum property)
It means line joining AO to D is perpendicular to BC.
Hence, all the perpendicular pass through the same point, i.e., they are concurrent.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a22videos
CIRCLE
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b19videos
CIRCLE
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
Similar Questions
Show that the altitudes of a triangle are concurrent
View SolutionProve that the medians of a triangle are concurrent.
View SolutionShow, by vector methods, that the angularbisectors of a triangle are concurrent and find an expression for the position vector of the point of concurrency in terms of the position vectors of the vertices.
View SolutionProve using vectors: Medians of a triangle are concurrent.
View SolutionUsing vector method, prove that the angel in a semi circle is a right angle.
View SolutionUsing vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View SolutionUsing vector method, prove that the following points are collinear:
A(1,2,7) B(2,6,3) C(3,10,-1)View SolutionUsing vector method, prove that the following points are collinear:
A(6,-7,-1) B(2,-3,1) C(4,-5,0)View SolutionUsing vector method, prove that the following points are collinear: A(-3,-2-5),B(1,2,3)and C(3,4,7)
View SolutionUsing vector method, prove that the following points are collinear:
A(2,-1,3) B(4,3,1) C(3,1,2)View Solution

