Two diameters of a circle intersect each other at right angles. Prove that the quadrilateral formed by joining their end-points is a square.
The correct Answer is:NA
NA
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10c
20 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (very Short Answer Question)
10 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
If two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a
View SolutionThe diagonals of a rectangle intersect each other at right angles. Prove that the rectangle is a square.
View SolutionWill two diameters of a circle always intersect?
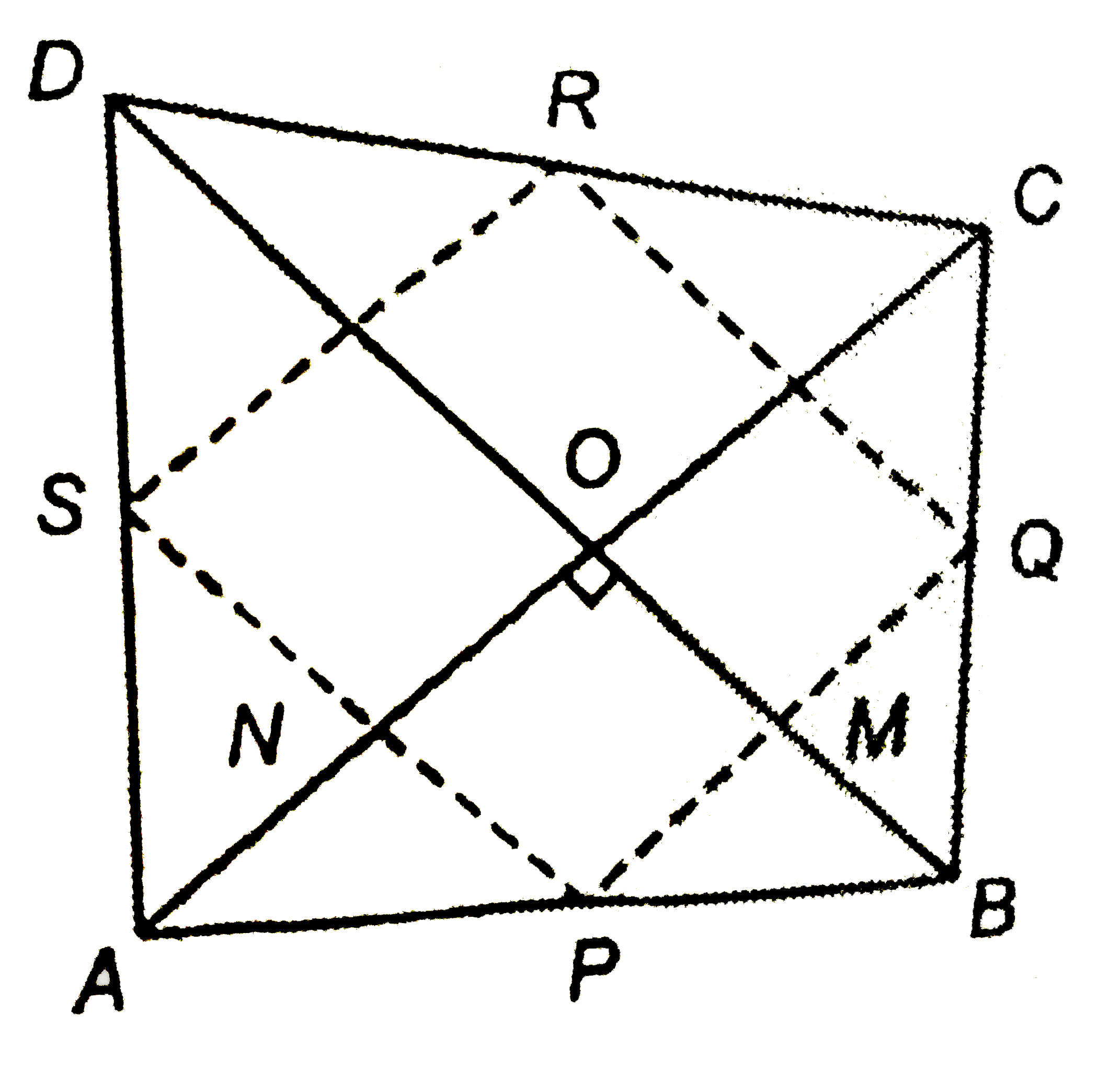
View SolutionThe diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionIf the diagonals of a quadrilateral bisect each other at right angle, prove that the quadrilateral is a rhombus.
A rhombus has all its four sides equal.
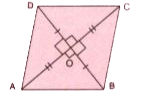
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View Solution
