If f(x) is defined as follows:
f(x)=⎧⎪⎨⎪⎩1x>0−1x<00x=0
Then show that limx→0f(x) does not exist.
To show that the limit limx→0f(x) does not exist, we will evaluate the left-hand limit and the right-hand limit of the function f(x) as x approaches 0.
Step 1: Define the function
The function f(x) is defined as follows:
- f(x)=1 when x>0
- f(x)=−1 when x<0
- f(x)=0 when x=0
Step 2: Calculate the left-hand limit
The left-hand limit as x approaches 0 is given by:
limx→0−f(x)
For values of x that are slightly less than 0 (i.e., x<0), we have:
f(x)=−1
Thus, the left-hand limit is:
limx→0−f(x)=−1
Step 3: Calculate the right-hand limit
The right-hand limit as x approaches 0 is given by:
limx→0+f(x)
For values of x that are slightly greater than 0 (i.e., x>0), we have:
f(x)=1
Thus, the right-hand limit is:
limx→0+f(x)=1
Step 4: Compare the left-hand limit and right-hand limit
Now we compare the two limits:
- Left-hand limit: limx→0−f(x)=−1
- Right-hand limit: limx→0+f(x)=1
Since the left-hand limit and the right-hand limit are not equal:
−1≠1
Conclusion
Since the left-hand limit and right-hand limit as x approaches 0 are not equal, we conclude that the limit limx→0f(x) does not exist.
The function f(x) is defined as follows:
- f(x)=1 when x>0
- f(x)=−1 when x<0
- f(x)=0 when x=0
The left-hand limit as x approaches 0 is given by:
limx→0−f(x)
For values of x that are slightly less than 0 (i.e., x<0), we have:
f(x)=−1
Thus, the left-hand limit is:
limx→0−f(x)=−1
The right-hand limit as x approaches 0 is given by:
limx→0+f(x)
For values of x that are slightly greater than 0 (i.e., x>0), we have:
f(x)=1
Thus, the right-hand limit is:
limx→0+f(x)=1
Now we compare the two limits:
- Left-hand limit: limx→0−f(x)=−1
- Right-hand limit: limx→0+f(x)=1
−1≠1
Since the left-hand limit and right-hand limit as x approaches 0 are not equal, we conclude that the limit limx→0f(x) does not exist.
Topper's Solved these Questions
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX-13B
11 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX-13C
11 Videos
- LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise
30 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Miscellaneous Exercise
6 Videos
- LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - MISCELLANEOUS EXERCISE
14 Videos
Similar Questions
If f(x)=|x|x, then show that limx→0f(x) does not exist.
View SolutionIf f(x)={x−|x|x,x≠0,2,x=0, show that limx→0 f(x) does not exist.
View SolutionIf f(x) is defined as
f(x)=⎧⎪⎨⎪⎩x0≤x≤11x=12−xx>1
then show that limX→1f(x)=1
View SolutionLet f(x) be a function defined by f(x)={3x|x|+2xx≠00x=0
Show that limx→0f(x) does not exist.
View SolutionIf f(x)={x−|x|x,x≠02, x=0,show that limx→0f(x) does not exist.
View SolutionLetf(x)={x+1, ifx≥0x−1, ifx<0.Then prove thatlimx→0f(x) does not exist.
View SolutionGiven f(x)={x+|x|xx≠0−2x=0 show that limx→0f(x) does not exist.
View SolutionEvaluate limx→0f(x), where
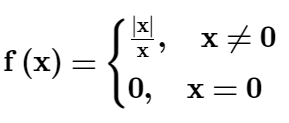
View SolutionIf f(x)={xsin(1x)x≠00x=0 Then, limx→0f(x)
View SolutionIf f(x) is defined as
f(x)={2x+3x≤03x+3x≥0
then evaluate : limx→0f(x)andlimx→1f(x)
View Solution
