In figure, DE||ABandBD||BEF. Prove that DC2=CF×AC
To prove that DC2=CF×AC, we will use the properties of similar triangles and the Basic Proportionality Theorem (also known as Thales' theorem).
1. Identify the triangles: We have triangle ABC with line DE parallel to AB and line BD parallel to BEF.
2. Apply the Basic Proportionality Theorem in Triangle ABC:
Since DE∥AB, by the Basic Proportionality Theorem, we have:
CDCA=CECB(1)
3. Apply the Basic Proportionality Theorem in Triangle CDB:
Since BD∥BEF, again by the Basic Proportionality Theorem, we have:
CFCD=CECB(2)
4. Equate the two ratios:
From equations (1) and (2), we know that both ratios equal CECB. Therefore, we can set the two ratios equal to each other:
CDCA=CFCD
5. Cross-multiply:
Cross-multiplying gives us:
CD×CD=CA×CF
or
CD2=CF×AC
6. Conclusion:
Thus, we have proved that:
DC2=CF×AC
Since DE∥AB, by the Basic Proportionality Theorem, we have:
CDCA=CECB(1)
Since BD∥BEF, again by the Basic Proportionality Theorem, we have:
CFCD=CECB(2)
From equations (1) and (2), we know that both ratios equal CECB. Therefore, we can set the two ratios equal to each other:
CDCA=CFCD
Cross-multiplying gives us:
CD×CD=CA×CF
or
CD2=CF×AC
Thus, we have proved that:
DC2=CF×AC
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In the following figure, DE||AC and DC||AP. Prove that : BEEC=BCCP
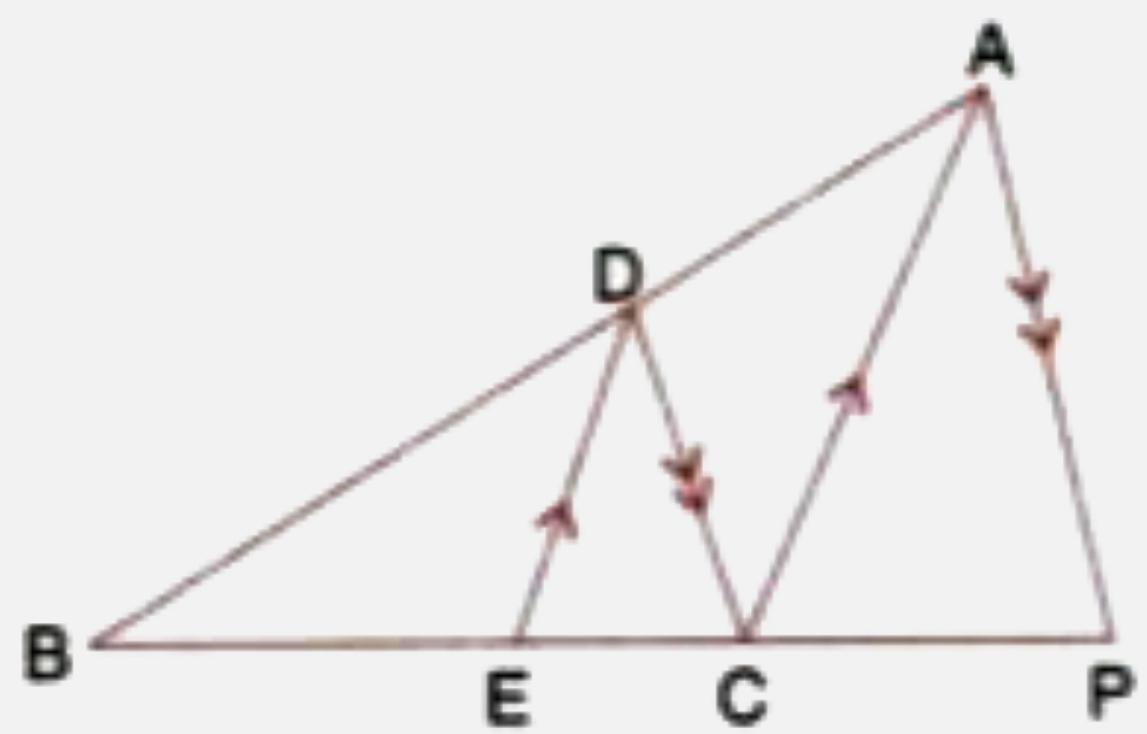
View SolutionIn the given figure DE||AC and DC||AP. Prove that BEEC=BCCP

View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC

View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC

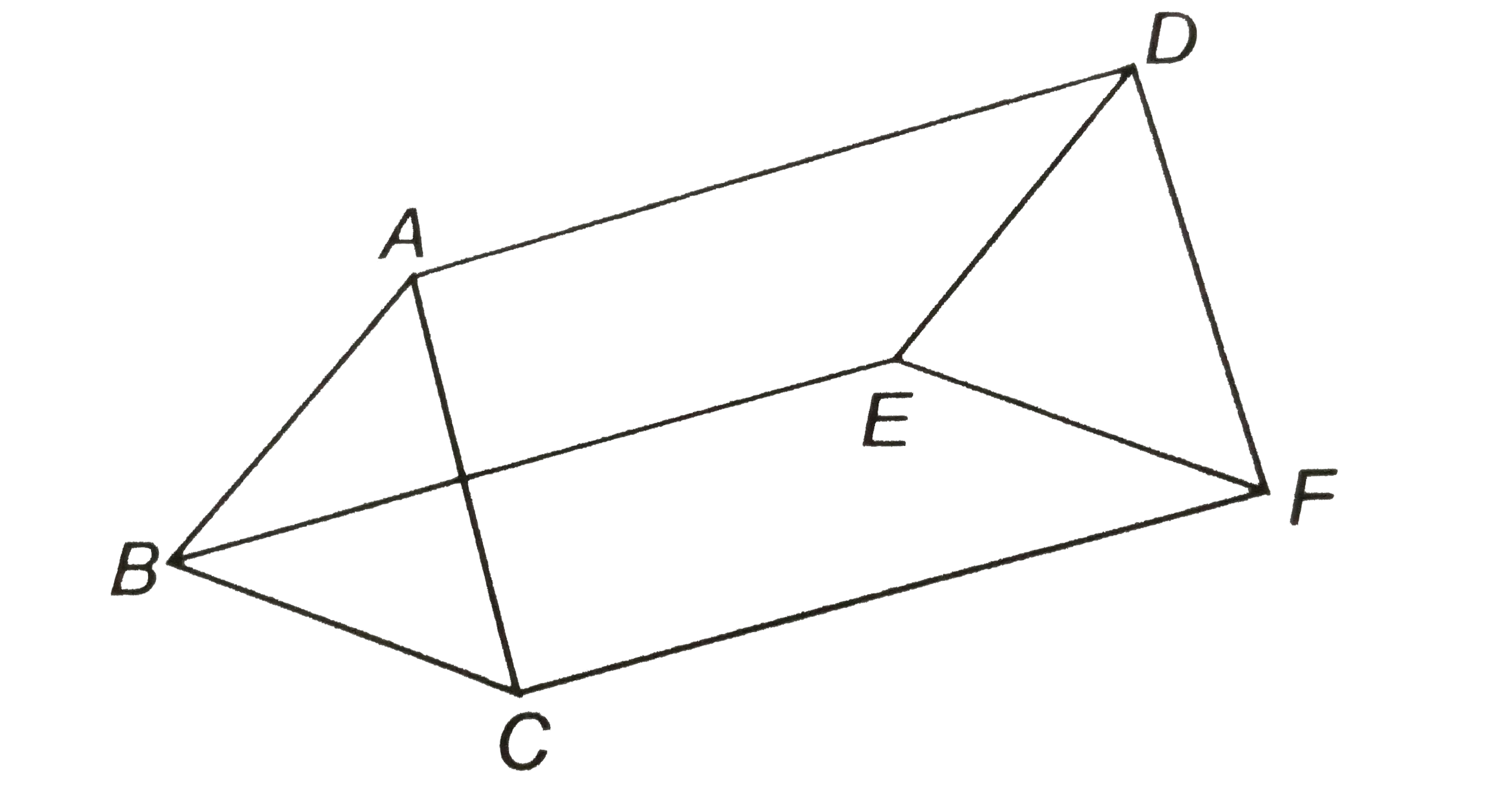
View SolutionIn figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=EF.
View SolutionIn theadjoining figure, ∠DAB=∠ABC and AD=BC prove that BD=AC.

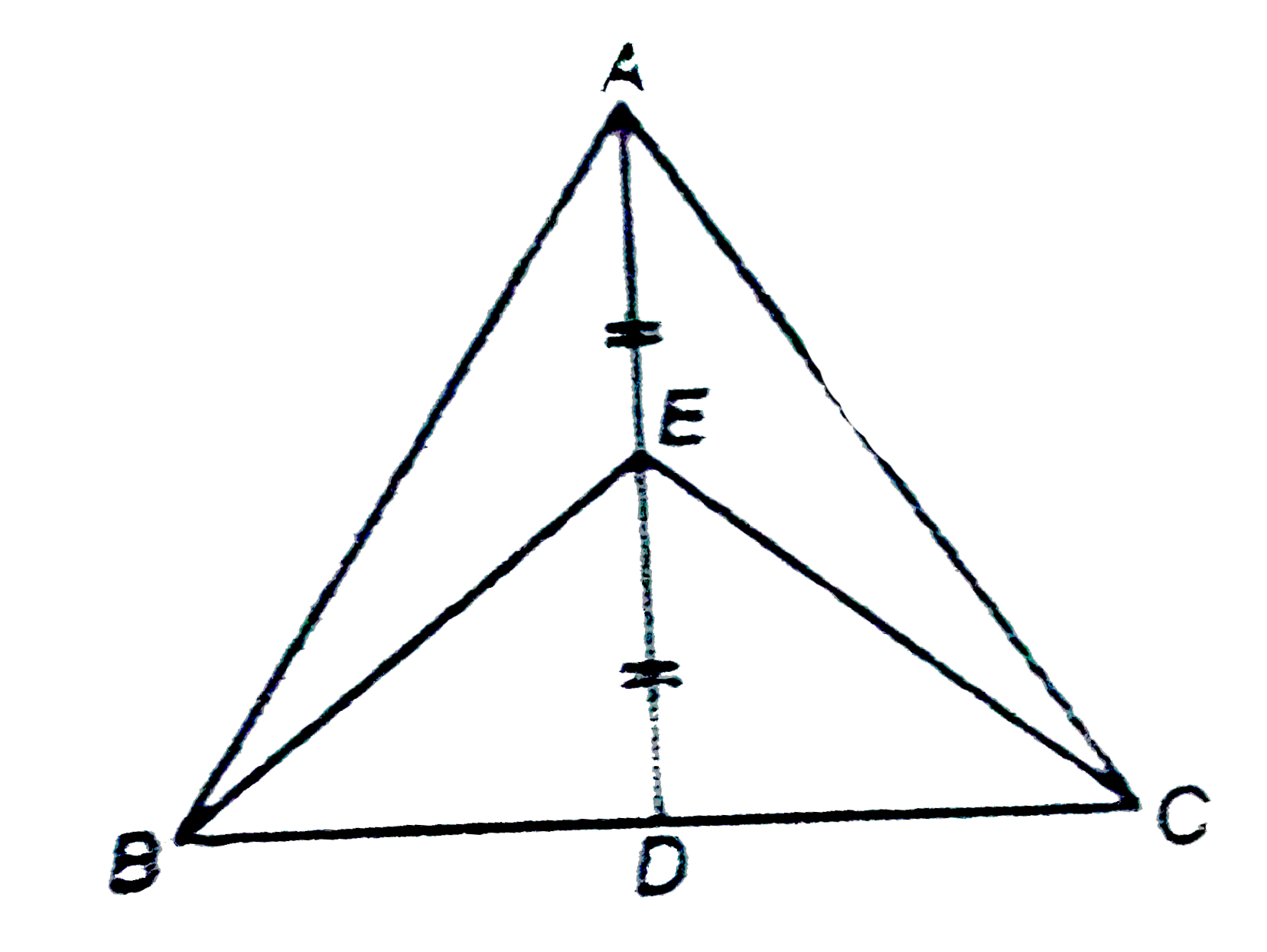
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
View SolutionIn Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
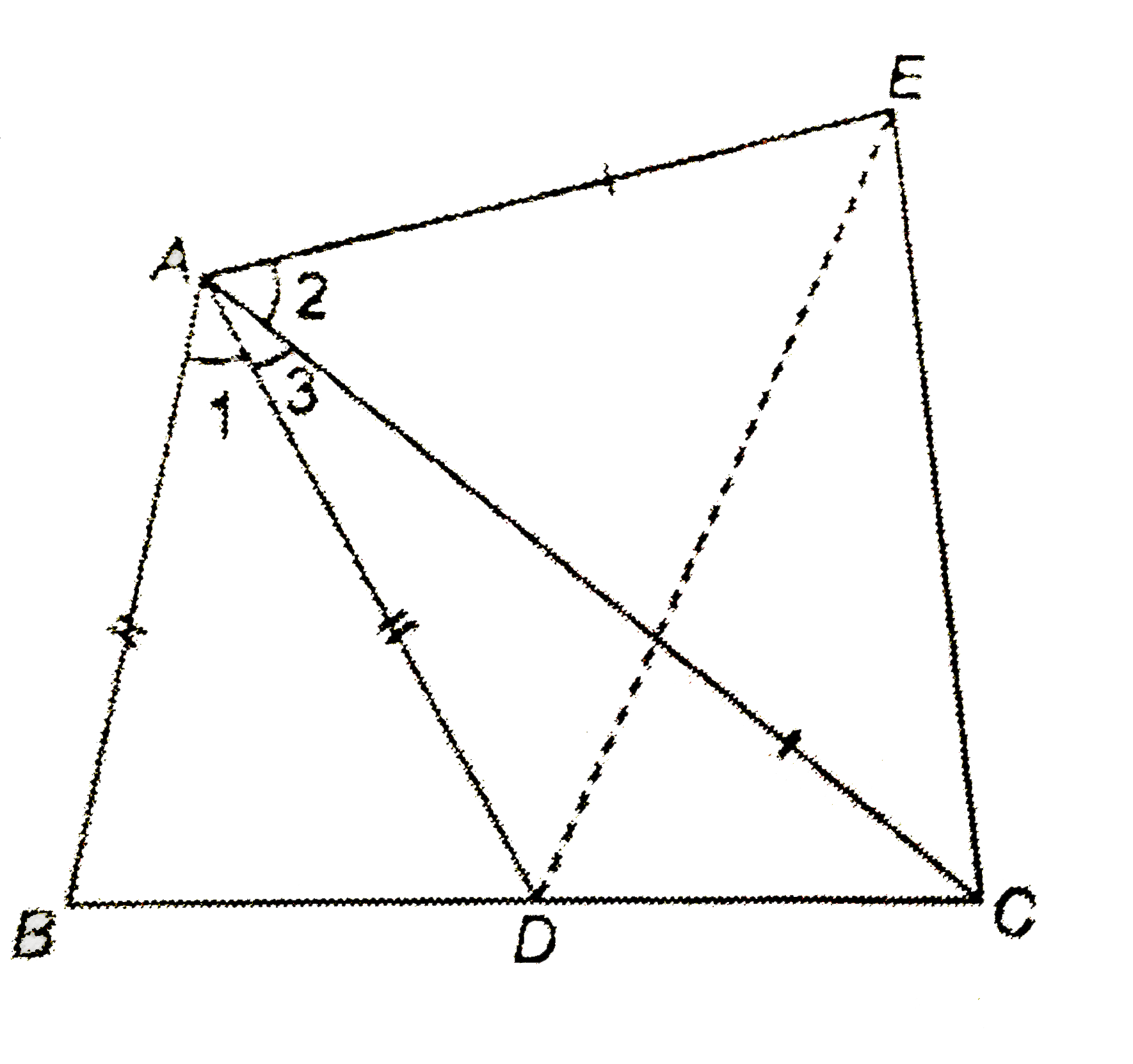
View SolutionIn the given figure, AC=AE,AB=AD and ∠BAD=∠EAC. Prove that BC=DE.
View SolutionΔABD is a right triangle, right-angled at A and AC⊥BD. Prove that AB2=BC×BD.
View Solution
