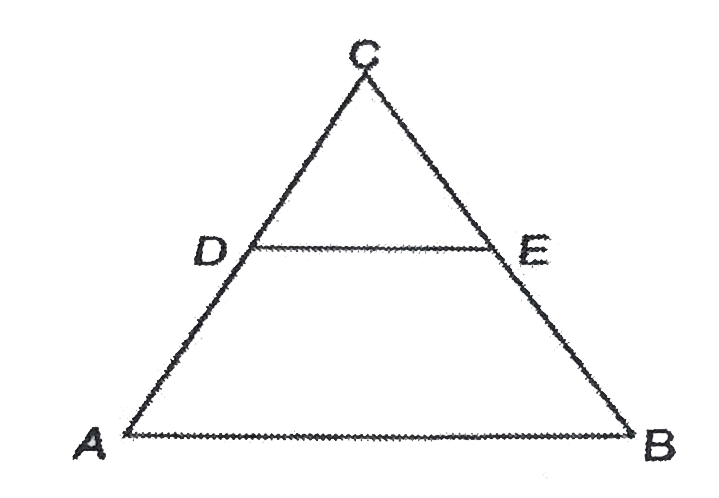
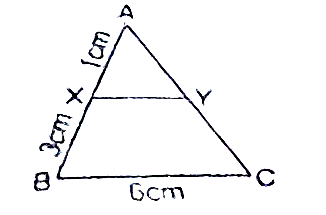
In the given figure if DE||BC, find the value of x.
To solve the problem where DE is parallel to BC, we can use the properties of similar triangles. Here’s the step-by-step solution:
Step 1: Identify the triangles
Since DE is parallel to BC, we can consider triangles ADE and ABC.
Step 2: Use the Corresponding Angles Postulate
By the Corresponding Angles Postulate, we know that:
- Angle ADE = Angle ABC (corresponding angles)
- Angle ACB = Angle DAE (corresponding angles)
Step 3: Establish similarity of triangles
Since two pairs of corresponding angles are equal, we can conclude that triangle ADE is similar to triangle ABC by the Angle-Angle (AA) criterion of similarity.
Step 4: Set up the proportion
From the similarity of triangles, we can set up the following proportion based on the sides of the triangles:
ADAB=DEBC
Step 5: Substitute the known values
From the problem, we have:
- AD = 3 cm
- AB = 7 cm
- DE = 2 cm
- BC = x cm (the value we want to find)
Substituting these values into the proportion gives us:
37=2x
Step 6: Cross-multiply to solve for x
Cross-multiplying gives us:
3x=14
Step 7: Solve for x
Now, divide both sides by 3 to isolate x:
x=143≈4.67 cm
Thus, the value of x is approximately 4.67 cm.
Final Answer
The value of x is 4.67 cm.
---
Since DE is parallel to BC, we can consider triangles ADE and ABC.
By the Corresponding Angles Postulate, we know that:
- Angle ADE = Angle ABC (corresponding angles)
- Angle ACB = Angle DAE (corresponding angles)
Since two pairs of corresponding angles are equal, we can conclude that triangle ADE is similar to triangle ABC by the Angle-Angle (AA) criterion of similarity.
From the similarity of triangles, we can set up the following proportion based on the sides of the triangles:
ADAB=DEBC
From the problem, we have:
- AD = 3 cm
- AB = 7 cm
- DE = 2 cm
- BC = x cm (the value we want to find)
37=2x
Cross-multiplying gives us:
3x=14
Now, divide both sides by 3 to isolate x:
x=143≈4.67 cm
The value of x is 4.67 cm.
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
In the given figure, AB∣∣CD. Find the value of x
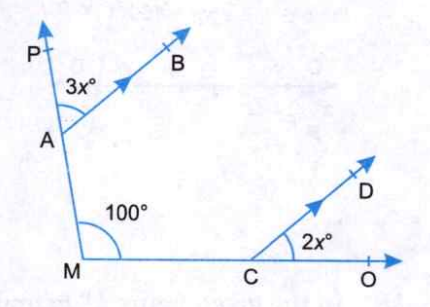 A20B25C40D60
A20B25C40D60
In the given figure, find the value of x. What is the measure of ∠COD?
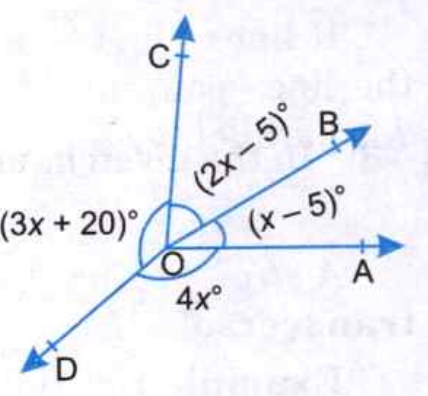
View SolutionInthegivenfigure,f∈dthevalueofx+y
View SolutionInthegivenfigure,f∈dthevalueofx
View SolutionInthegivenfigure,f∈dthevalueofx
View SolutionInthegivenfigure,f∈dthevalueofx
View SolutionInthegivenfigure,f∈dthevalueofx
View SolutionInthegivenfigure,f∈dthevalueofx
View Solution