In the figure AC||BD , prove that:
(i)△ACE~△BDE(ii)AECE=BEDE
To solve the problem, we need to prove two things:
1. Triangle ACE is similar to triangle BDE (denoted as triangle ACE ~ triangle BDE).
2. The ratio of the segments AE to CE is equal to the ratio of the segments BE to DE, i.e., (AE)/(CE) = (BE)/(DE).
Let's go through the proof step by step.
Step 1: Identify the given information
We are given that AC is parallel to BD. This means that any transversal line (like AB or CD) that intersects these two parallel lines will create corresponding angles that are equal.
Step 2: Establish the angles
Since AC || BD, we can use the property of alternate interior angles:
- Angle CAE = Angle DBE (by alternate interior angles)
- Angle AEC = Angle BED (by vertical opposite angles)
- Angle ACE = Angle BDE (by alternate interior angles)
Step 3: State the similarity of triangles
From the above angles, we have:
- Angle CAE = Angle DBE
- Angle AEC = Angle BED
- Angle ACE = Angle BDE
Since all three pairs of angles are equal, we can conclude by the Angle-Angle-Angle (AAA) similarity criterion that:
- Triangle ACE ~ Triangle BDE
Step 4: Use the property of similar triangles
Since the triangles are similar, the ratios of their corresponding sides are equal:
- AE/BE = CE/DE = AC/BD
Step 5: Rearranging the ratios
From the equality of the ratios, we can express:
- AE/CE = BE/DE
This gives us the required result.
Conclusion
Thus, we have proved both parts:
1. Triangle ACE is similar to triangle BDE.
2. (AE)/(CE) = (BE)/(DE).
2. The ratio of the segments AE to CE is equal to the ratio of the segments BE to DE, i.e., (AE)/(CE) = (BE)/(DE).
We are given that AC is parallel to BD. This means that any transversal line (like AB or CD) that intersects these two parallel lines will create corresponding angles that are equal.
Since AC || BD, we can use the property of alternate interior angles:
- Angle CAE = Angle DBE (by alternate interior angles)
- Angle AEC = Angle BED (by vertical opposite angles)
- Angle ACE = Angle BDE (by alternate interior angles)
From the above angles, we have:
- Angle CAE = Angle DBE
- Angle AEC = Angle BED
- Angle ACE = Angle BDE
- Triangle ACE ~ Triangle BDE
Since the triangles are similar, the ratios of their corresponding sides are equal:
- AE/BE = CE/DE = AC/BD
From the equality of the ratios, we can express:
- AE/CE = BE/DE
Thus, we have proved both parts:
1. Triangle ACE is similar to triangle BDE.
2. (AE)/(CE) = (BE)/(DE).
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In the given figure AC = BD, prove that AB = CD.

View SolutionIn the given figure, AB = AC. Prove that AF is greater than AE.
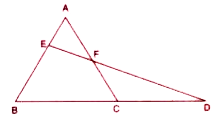
View SolutionIn the given figure AB=AC and AD=AE. Prove that (i) ΔABD≅ΔACE and (ii) BE=DC
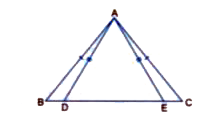
View SolutionIn the given figure : AB//FD, AC//GE and BD = CE, prove that :
(i) BG = DF
(ii) CF = EG
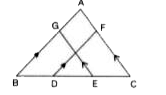
View SolutionIn the given figure AC=AE
Show that
(i) CP=EP
(ii) BP=DP
View SolutionFrom the following figure, prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View SolutionIn the given figure below, if AC = BD then prove that AB = CD.

View SolutionIn the given figure we have AO=BO and CO=DO. Prove that :
(i) ΔAOC≅ΔBOD
AC=BD

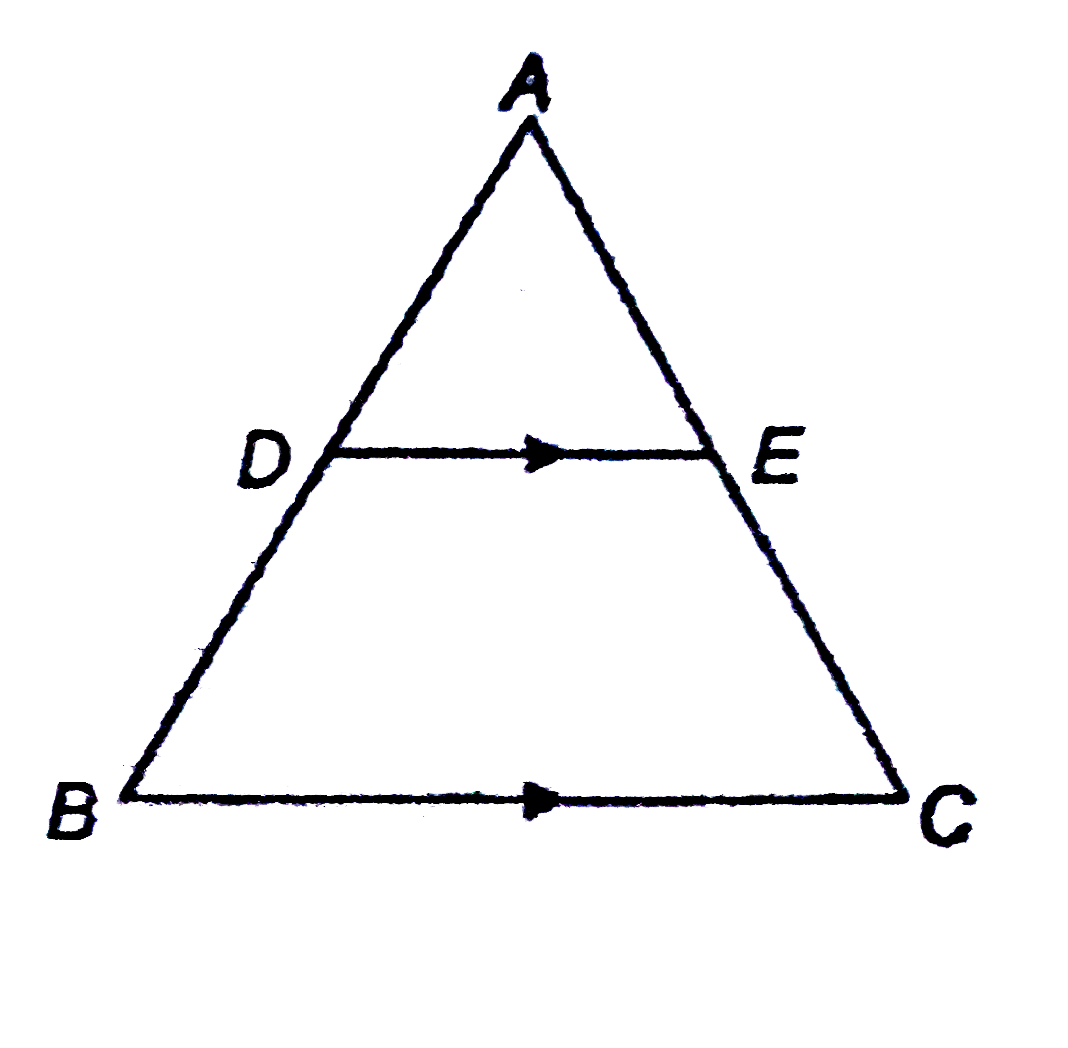
View SolutionIn the adjoining figure DE||BC and D divides AB in the ratio 2:3 find.
(i) AEEC (ii) AEAC
View SolutionIn the given figure, AB//EC,AB=ACandAE bisects ∠DAC. Prove that:
(i) ∠EAC=∠ACB
(ii) ABCE is a parallelogram.
 .
.
View Solution
