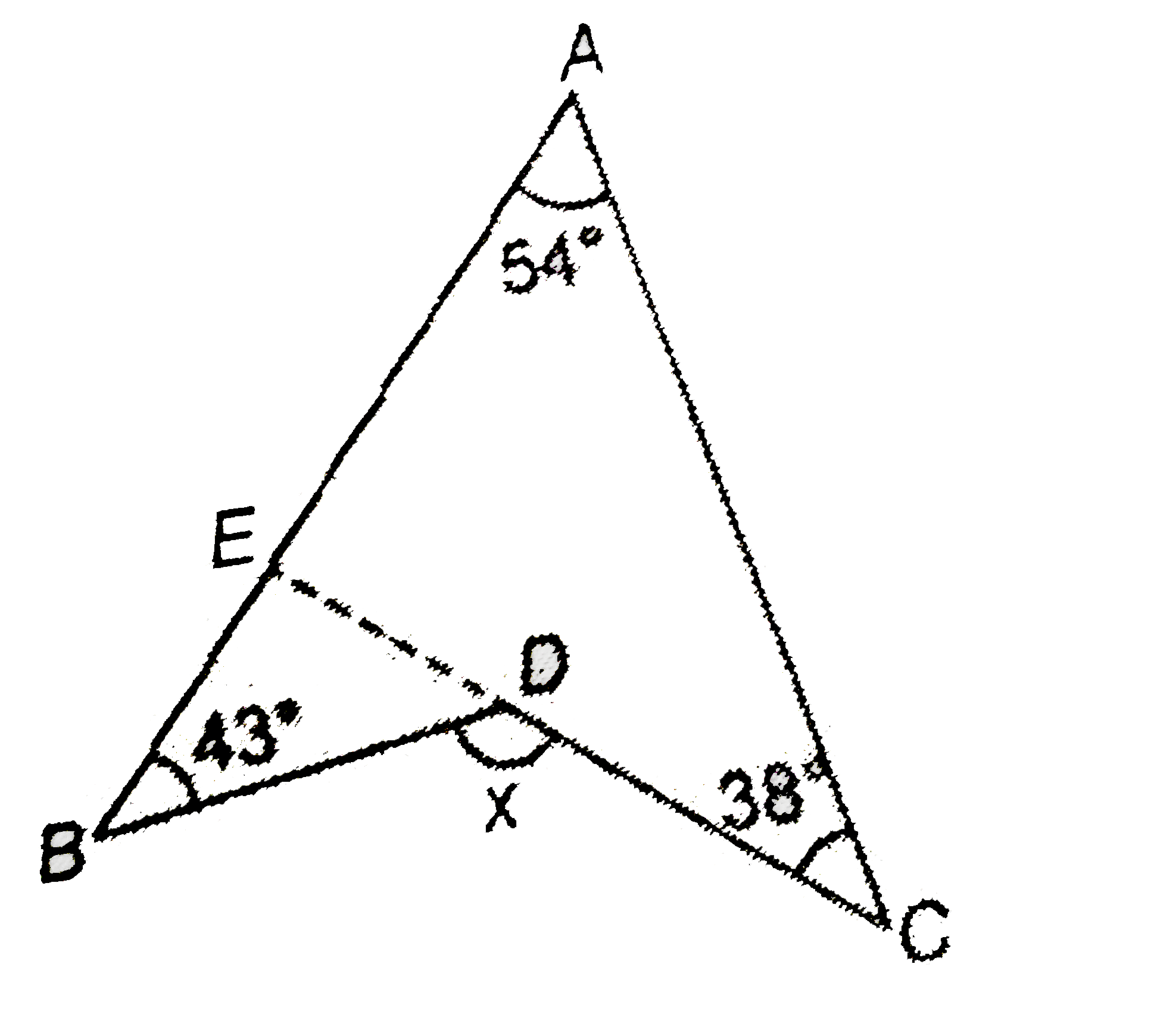
In the adjoining figure if a= 18 , b= 12,c = 14 and d=8 , what is the measure of x?
To solve the problem, we need to find the measure of x using the given values and the properties of similar triangles.
1. Identify the Given Values:
- a=QR=18cm
- b=PR=12cm
- c=PQ=14cm
- d=SR=8cm
2. Set Up Ratios Using Similar Triangles:
- From the triangles △PRS and △QRP, we can set up the following ratios based on the sides:
PRQR=ba=1218=23
- Similarly, we can find:
SRPR=db=812=23
3. Establish the Proportionality:
- Since both ratios are equal, we can write:
PRQR=SRPR
- This means:
1218=812
4. Use the Side-Angle-Side (SAS) Similarity:
- By the SAS similarity criterion, we can conclude:
PRQR=SRPR=PSQP
- Here, PS=x and QP=c=14.
5. Set Up the Equation:
- From the similarity, we have:
x14=23
6. Cross-Multiply to Solve for x:
- Cross-multiplying gives:
3x=2×14
3x=28
- Now, divide both sides by 3:
x=283
7. Final Answer:
- Therefore, the measure of x is:
x=283cm
- a=QR=18cm
- b=PR=12cm
- c=PQ=14cm
- d=SR=8cm
- From the triangles △PRS and △QRP, we can set up the following ratios based on the sides:
PRQR=ba=1218=23
- Similarly, we can find:
SRPR=db=812=23
- Since both ratios are equal, we can write:
PRQR=SRPR
- This means:
1218=812
- By the SAS similarity criterion, we can conclude:
PRQR=SRPR=PSQP
- Here, PS=x and QP=c=14.
- From the similarity, we have:
x14=23
- Cross-multiplying gives:
3x=2×14
3x=28
- Now, divide both sides by 3:
x=283
- Therefore, the measure of x is:
x=283cm
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar14videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a24videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions4videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
Using the adjoining figure, find a+b+c+d.
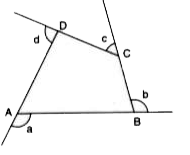 A180∘B360∘C270∘D380∘
A180∘B360∘C270∘D380∘ - Question 2 - Select One
In the figure, the angles A, B, C of the triangle are in the ratio 5 : 12 : 13. What is the measure of angle A?
 A15B27C30D34
A15B27C30D34
In the adjoining figure, find AC . (FIGURE)
View SolutionFrom the adjoining figure, find :
x∘View SolutionFrom the adjoining figure, find :

x∘View SolutionIn the adjoining figure, DE is parallel to BC and AD=1cm, BD=2cm. What is the ratio of the area of △ABC to the area of △ADE?
View SolutionIn the adjoining figure , a=(7x+5)∘andb=(5x+23)∘. Calculate the values of c and d
 View Solution
View SolutionIn the adjacent figure, if AB=12cm, BC=8cm and AC=10cm , then AD= (a) 5cm (b) 4cm (c) 6cm (d) 7cm
View Solution