In △ABCthe bisector of ∠B meets AC at D. A line PQ||AC meets AB,BC and BD at P, Q and R respectively.
show that PR×BQ=QR×BP.
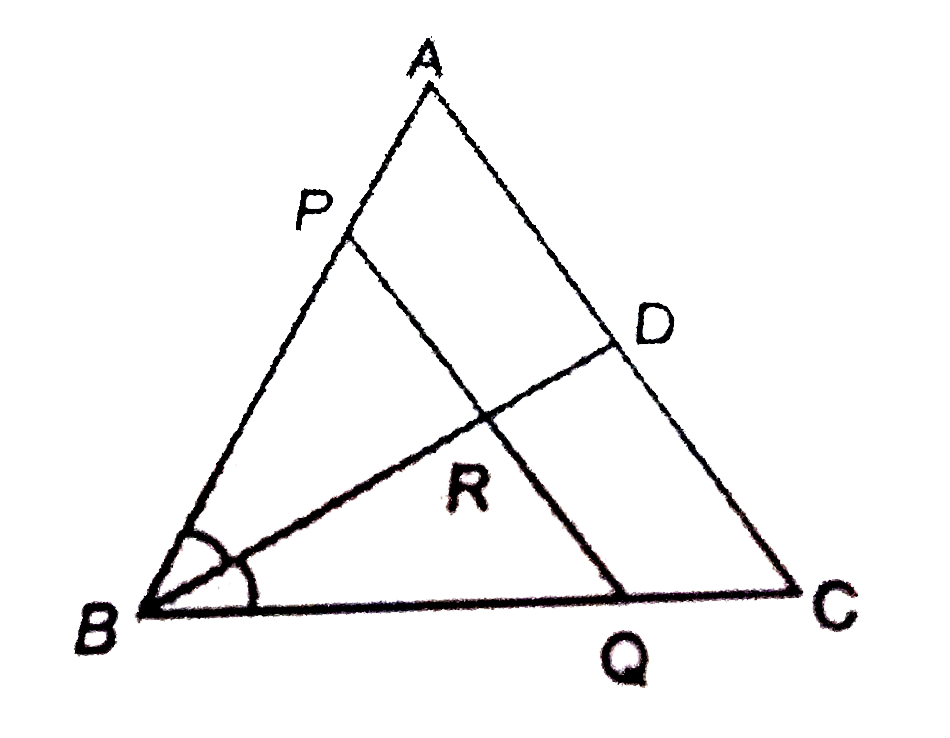
Step by step video & image solution for In triangleABCthe bisector of angleB meets AC at D. A line PQ||AC meets AB,BC and BD at P, Q and R respectively. show that PRxxBQ = QRxxBP. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Eercise 6b
1 Video
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6b
29 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In ABC , the bisector of ∠B meets AC at D. A line PQ∣∣AC meets AB,BCandBD at P,QandR respectively. Show that (i) PR⋅BQ=QR⋅BP (ii) AB⋅CQ=BC⋅AP
View SolutionIn ΔABC,AB=AC and the bisectors of ∠B and ∠C meet AC and AB at point D and E respectively. Prove that BD=CE.
View SolutionIn the given PR is the bisector of ∠BPC.It meets BC and AD at points Q and R respectively. Prove that:
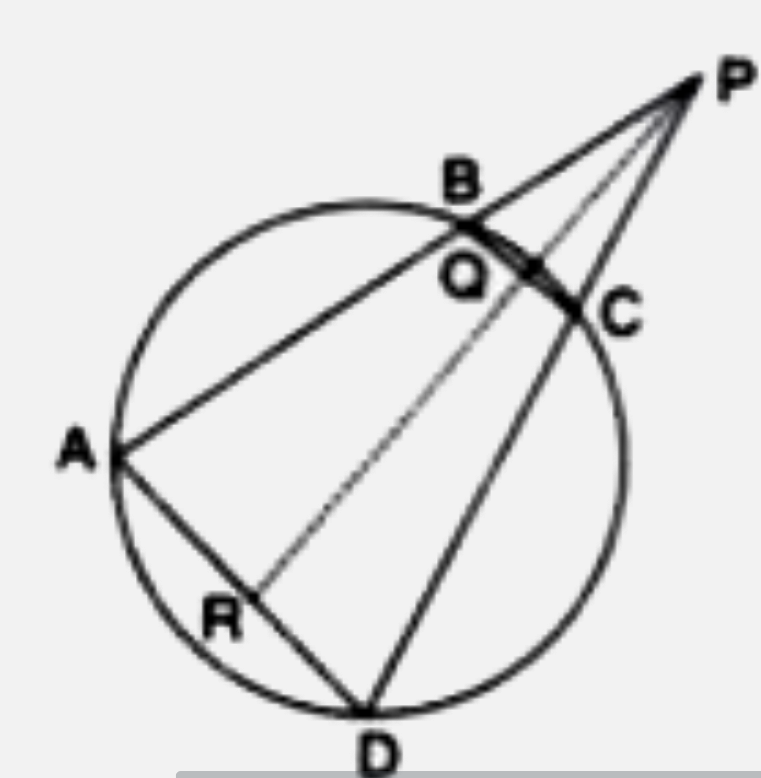
∠ARQ=∠BQR
View SolutionIn the given PR is the bisector of ∠BPC.It meets BC and AD at points Q and R respectively. Prove that:

angle ARQ + angle RQC = 180^(@)
View SolutionAD is a median of ΔABC . The bisector of ∠ADB and ∠ADC meet AB and AC in E and F respectively. Prove that EF||BC
View SolutionIn the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.

View SolutionIf in △ABC, AD is the bisector of ∠AandD lies on BC. If AB = 6.4 cm, AC = 8 cm, BD = 5.6 cm, find DC.
View SolutionTriangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : ABPQ=ADPM
View SolutionIn a tringle ABC, AB = AC and bisector of angle A meets BC at D. Prove that :
(i) ΔABD≅ΔACD (ii) AD is perpendicular to BC.
View SolutionXY is a line parallel to side BC of triangle ABC.BEllACandCF ll ABmeetXY∈EandFrespectively.Showtˆa r( A B E)=a r( A C F)dot
View Solution