In the adjoining figure: ∠PSQ=90∘ , PQ= 10 cm , QS = 6cm and RQ = 9cm . Calculate the length of PR.
The correct Answer is:17 cm
To solve the problem step by step, we will use the Pythagorean theorem in two triangles: triangle PQS and triangle PRS.
Step 1: Identify the given values
- PQ=10cm
- QS=6cm
- RQ=9cm
- ∠PSQ=90∘
Step 2: Calculate PS using the Pythagorean theorem in triangle PQS
In triangle PQS, we can apply the Pythagorean theorem:
PQ2=PS2+QS2
Substituting the given values:
102=PS2+62
This simplifies to:
100=PS2+36
Now, isolate PS2:
PS2=100−36
PS2=64
Taking the square root gives:
PS=√64=8cm
Step 3: Calculate RS
Next, we need to find RS. Since RS=RQ+QS:
RS=9cm+6cm=15cm
Step 4: Calculate PR using the Pythagorean theorem in triangle PRS
Now we can apply the Pythagorean theorem in triangle PRS:
PR2=PS2+RS2
Substituting the values we found:
PR2=82+152
Calculating the squares:
PR2=64+225
Adding these values gives:
PR2=289
Taking the square root:
PR=√289=17cm
Final Answer
The length of PR is 17cm.
---
- PQ=10cm
- QS=6cm
- RQ=9cm
- ∠PSQ=90∘
In triangle PQS, we can apply the Pythagorean theorem:
PQ2=PS2+QS2
Substituting the given values:
102=PS2+62
This simplifies to:
100=PS2+36
Now, isolate PS2:
PS2=100−36
PS2=64
Taking the square root gives:
PS=√64=8cm
Next, we need to find RS. Since RS=RQ+QS:
RS=9cm+6cm=15cm
Now we can apply the Pythagorean theorem in triangle PRS:
PR2=PS2+RS2
Substituting the values we found:
PR2=82+152
Calculating the squares:
PR2=64+225
Adding these values gives:
PR2=289
Taking the square root:
PR=√289=17cm
The length of PR is 17cm.
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise very shot Questions
1 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Very Short Questions
9 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6c
10 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In the figure: ∠PSQ=90∘,PQ=10cm,QS=6cmand RQ=9cm. Find the value of PR.

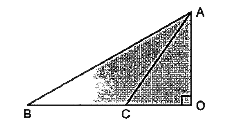
View SolutionIn triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC
View SolutionIn the figure, given below, PQR is a right angled triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1:2. Calculate the lengths of PR and QR.

View SolutionIn the given figure , ∠QPR=90∘ QR = 26 cm PM = 6cm, MR = 8cm and ∠PMR=90∘ . Find the area of triangle PQR.

View SolutionIn the adjoining figure, AB=8cm,DM=6cmandBC=6cm. Find the length of DN

View SolutionIn the given figure, ∠PQR=∠PST=90∘, PQ = 5cm and PS = 2 cm.
Prove that △PQR ~△PST

View SolutionIn the adjoining figure PQ = PR and ∠PRQ=70∘ Find ∠QPR.
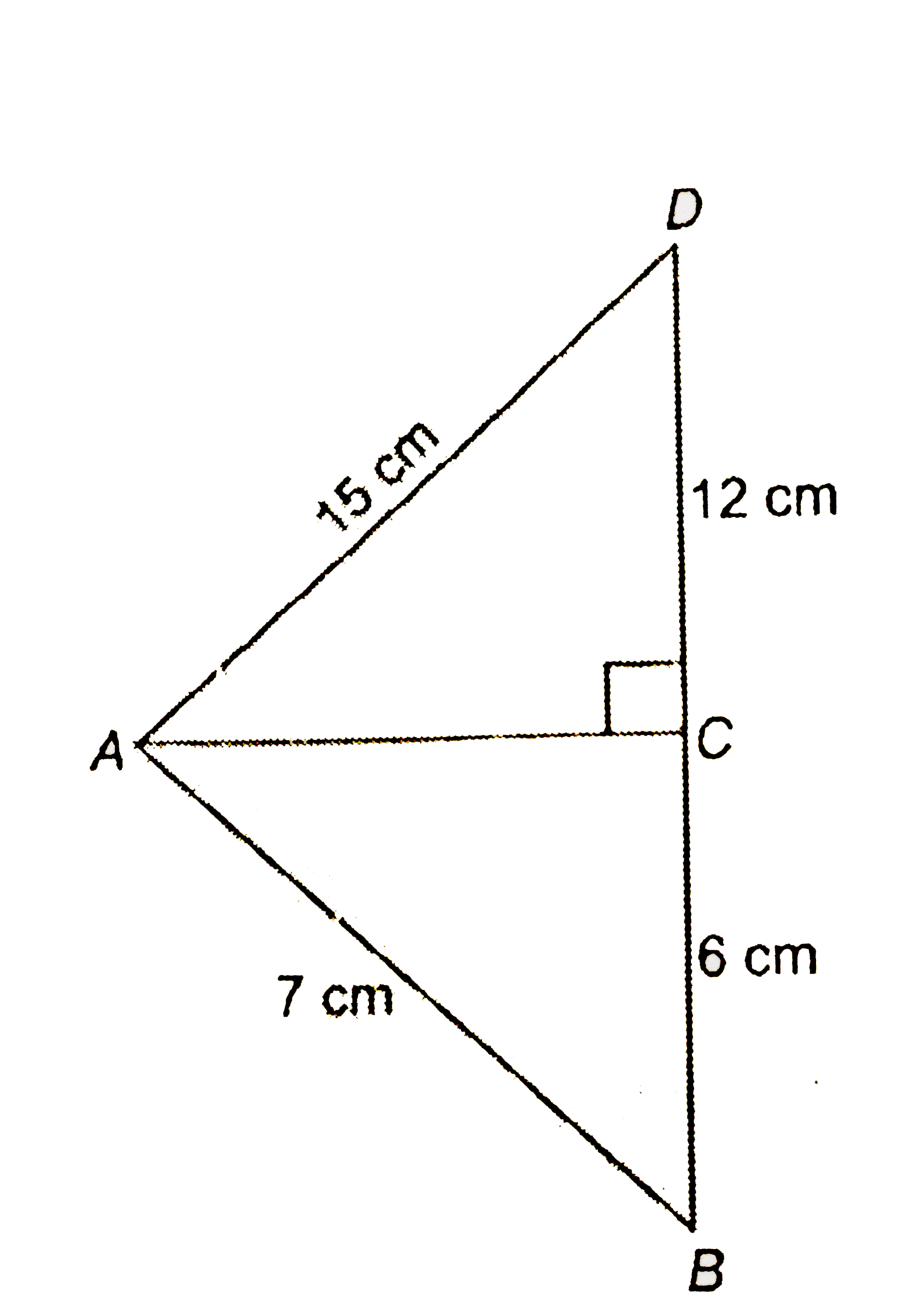
View SolutionIn the given figure ∠ACD=90∘
Ad=15 cm, DC=12 cm, AB=7 cm and BC=6 cm
Find the are of the shaded region.
View SolutionIn the given figures, ∠ABC=90∘=∠DECAC=15cmandAB=9cm. If the area of the quadrilateral ABCD is 72cm2: find the length of DE.
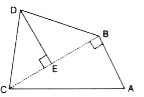
View SolutionIn given figure, if ∠A=∠C, AB= 6 cm, BP = 15 cm, AP = 12 cm and CP= 4 cm, then find the lengths of PD and CD.

View Solution
