In a square ABCD, show that AC2=2AB2.
To show that AC2=2AB2 in a square ABCD, we will use the Pythagorean theorem.
1. Identify the Square and its Properties:
- Let ABCD be a square.
- By definition of a square, all sides are equal. Therefore, we have AB=BC=CD=DA=a (where a is the length of one side of the square).
2. Identify the Diagonal:
- The diagonal AC connects vertices A and C.
3. Apply the Pythagorean Theorem:
- In triangle ADC, which is a right triangle (since ∠ADC=90∘), we can apply the Pythagorean theorem:
AC2=AD2+CD2
4. Substitute the Lengths:
- Since AD=AB=a and CD=BC=a (because all sides of the square are equal), we can substitute:
AC2=a2+a2
5. Simplify the Equation:
- Combine the terms:
AC2=2a2
6. Relate to AB:
- Since AB=a, we can express a2 as AB2:
AC2=2(AB2)
7. Conclusion:
- Thus, we have shown that:
AC2=2AB2
- Let ABCD be a square.
- By definition of a square, all sides are equal. Therefore, we have AB=BC=CD=DA=a (where a is the length of one side of the square).
- The diagonal AC connects vertices A and C.
- In triangle ADC, which is a right triangle (since ∠ADC=90∘), we can apply the Pythagorean theorem:
AC2=AD2+CD2
- Since AD=AB=a and CD=BC=a (because all sides of the square are equal), we can substitute:
AC2=a2+a2
- Combine the terms:
AC2=2a2
- Since AB=a, we can express a2 as AB2:
AC2=2(AB2)
- Thus, we have shown that:
AC2=2AB2
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Revision Exercise very shot Questions
Explore 1 Video
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Revision Exercise Very Short Questions
Explore 9 Videos
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Exercise 6c
Explore 10 Videos
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
In a rhombus ABCD, prove that AC2+BD2=4AB2
View SolutionIf P be any point in the plane of square ABCD, prove that
PA2+PC2=PB2+PD2
View SolutionIn a rectangle ABCD, prove that : AC2+BD2=AB2+BC2+CD2+DA2.
View SolutionConstruct a squre ABCD with AC = 6.2 cm.
View SolutionIn a quadrilateral ABCD, prove that :
(i) AB+BC+CD>DA
(ii) AB+BC+CD+DA>2AC
(iii) AB+BC+CD+DA>2BD
View SolutionThe following figures shows a triangle ABC in which AD is median and AE⊥BC.
Prove that : 2AB2+2AC2=4AD2+BC2
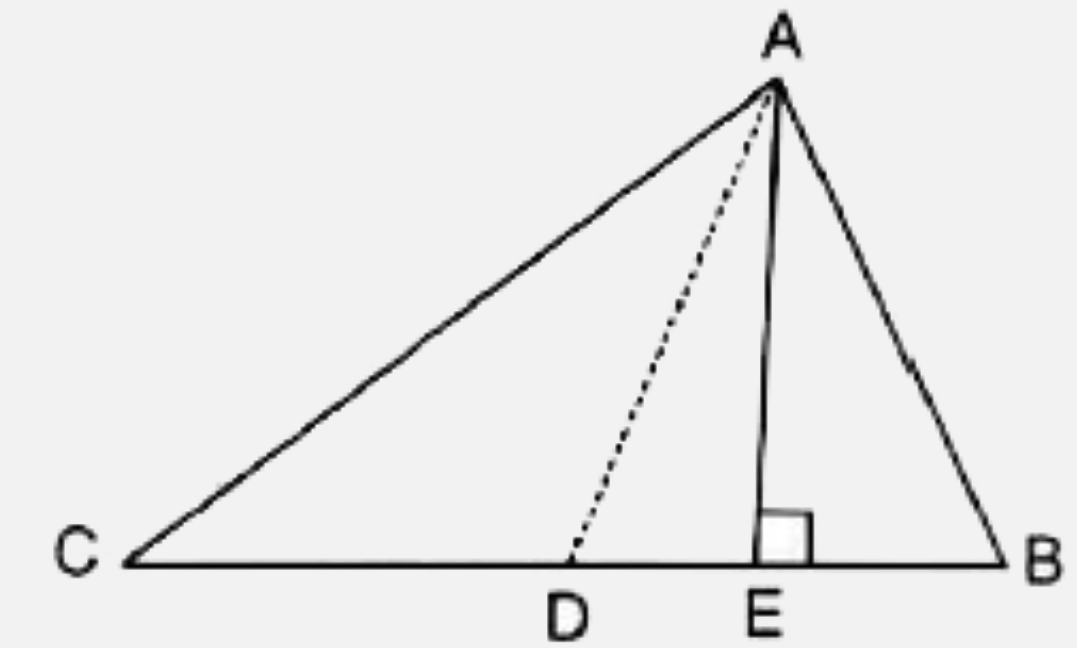
View SolutionIn a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
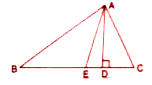
View SolutionThe given figure shows a triangle ABC, in which AB > AC. E is the mid-point of BC and AD is perpendicular to BC.
Prove that : AB2+AC2=2BE2+2AE2
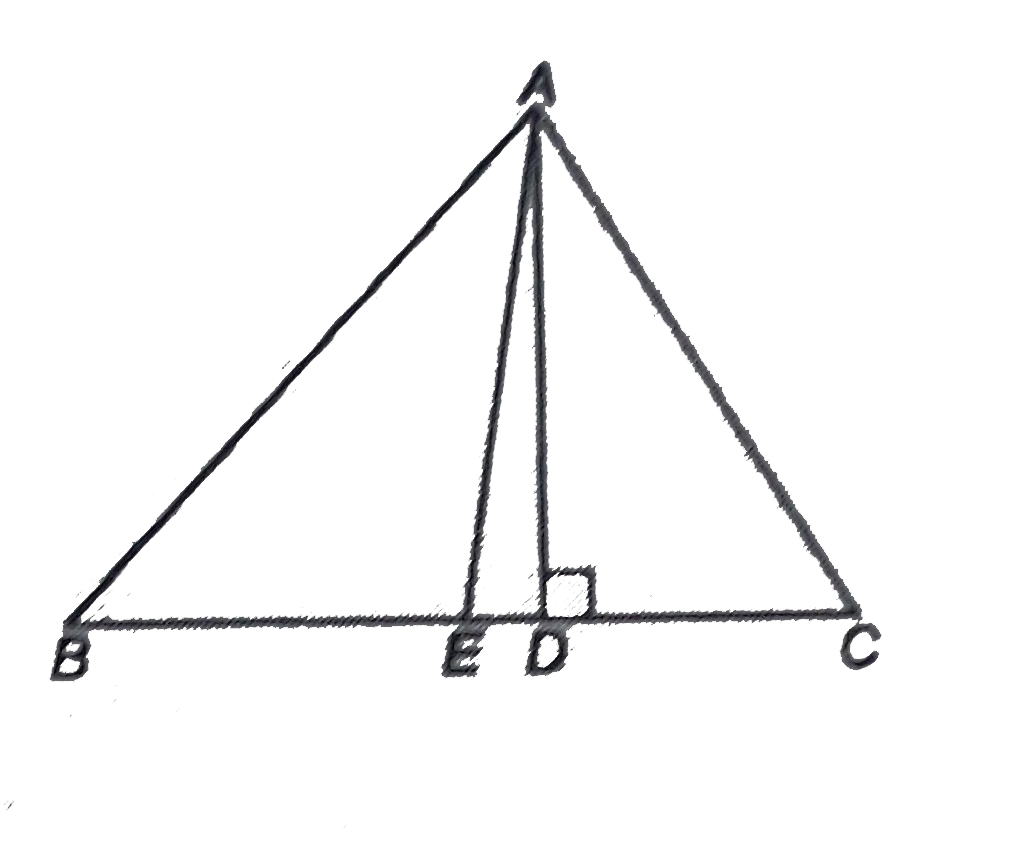
View SolutionThe given figure shows a triangle ABC, in which AB>AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that AB2−AC2=2BC×ED.
View SolutionIn a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that:
∠BDC=2∠POC
View Solution