The following figures shows a triangle ABC in which AD is median and AE⊥BC.
Prove that : 2AB2+2AC2=4AD2+BC2
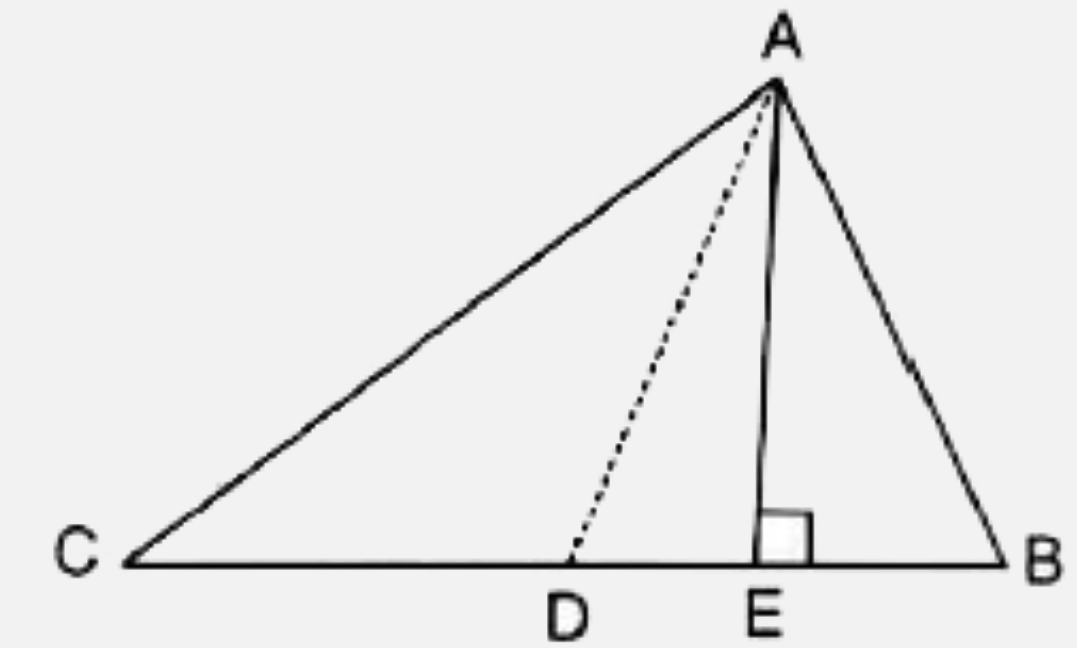
Step by step video & image solution for The following figures shows a triangle ABC in which AD is median and AE bot BC. Prove that : 2AB ^(2) + 2AC^(2) = 4AD^(2)+ BC^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - RECTILINEAR FIGURES
6 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - CONSTRUCTIONS OF POLYGONS
4 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - MID- POINT THEOREM
9 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
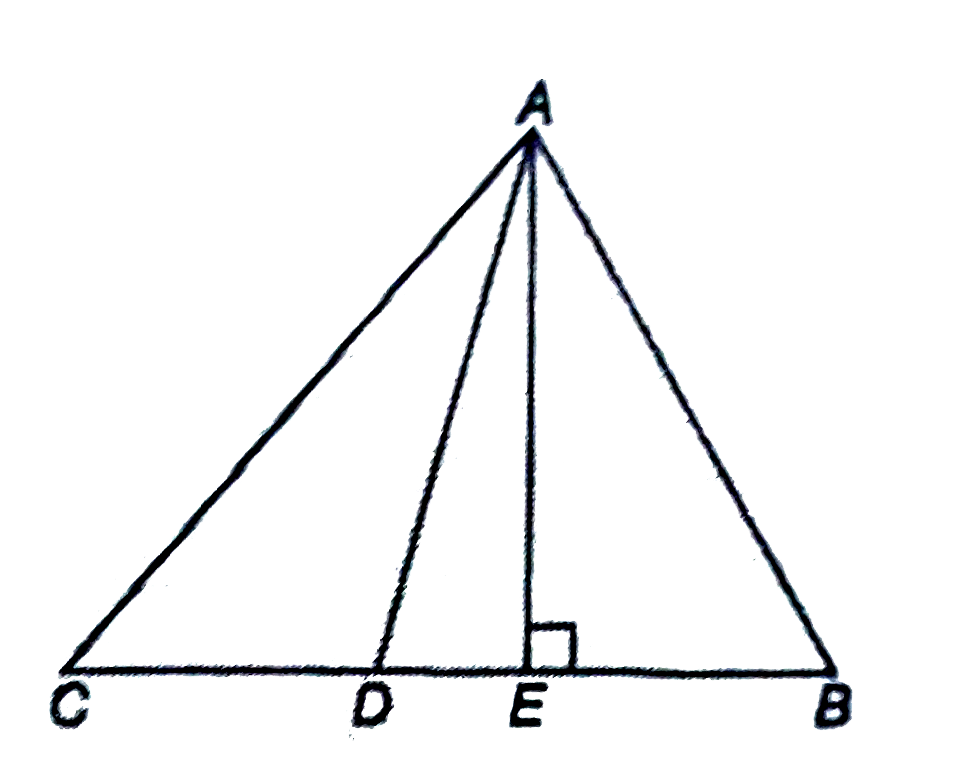
The following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
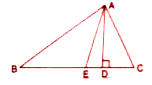
View SolutionThe given figure shows a triangle ABC, in which AB > AC. E is the mid-point of BC and AD is perpendicular to BC.
Prove that : AB2+AC2=2BE2+2AE2
View SolutionAD is a median of triangle ABC. Prove that : AB+BC+AC>2AD
View SolutionAD is a median of triangle ABC. Prove that : AB+AC>2AD
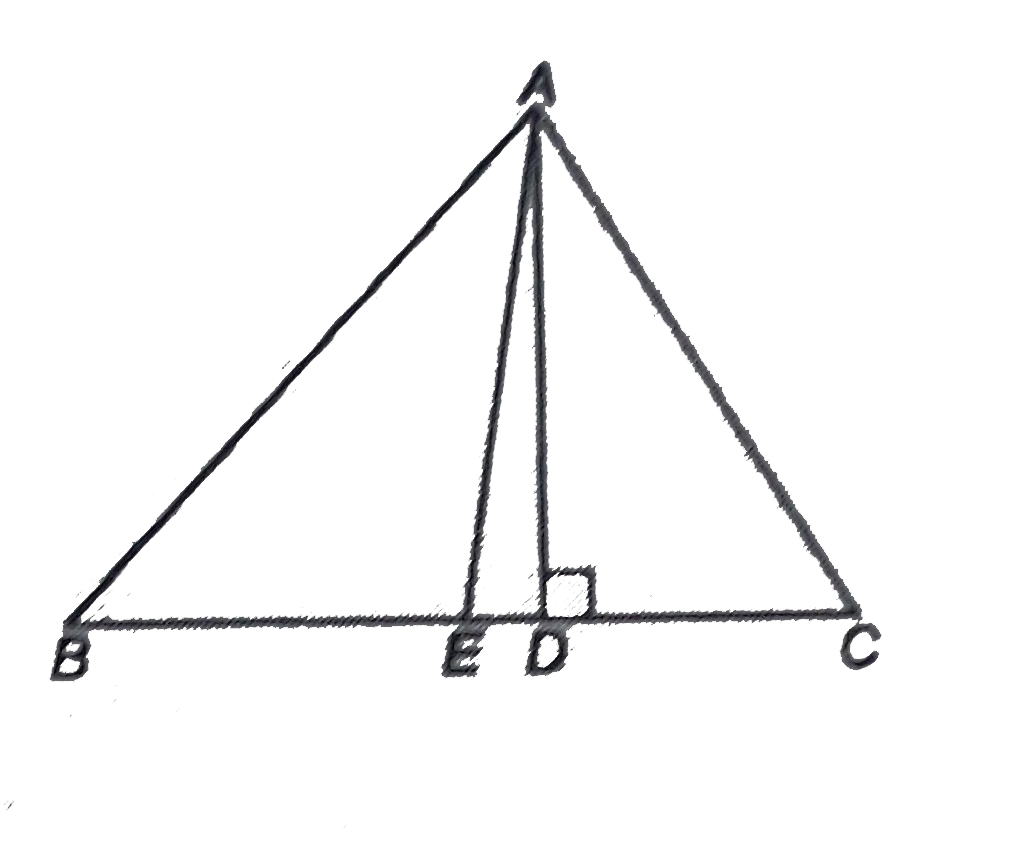
View SolutionThe given figure shows a triangle ABC, in which AB>AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that AB2−AC2=2BC×ED.
View SolutionIn an acute angled triangle ABC, AD is the median in it. then :
AD2 =
View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
CD×AB=CA×DE
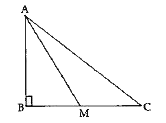
View SolutionABC is a triangle, right angled at B, M is a point on BC. Prove that :
AM2+BC2=AC2+BM2
View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
CA×CE=CB×CD

View Solution
