Prove that value of the function xy(y−x)=2a3 is minimum at x=a.
To prove that the value of the function xy(y−x)=2a3 is minimum at x=a, we will follow these steps:
Step 1: Rewrite the Function
The given function is:
xy(y−x)=2a3
Expanding this, we have:
xy2−x2y=2a3
Step 2: Differentiate the Function
To find the critical points, we need to differentiate the function with respect to x. We will apply the product rule for differentiation.
Differentiating xy2 and −x2y:
ddx(xy2)=y2+2xydydx
ddx(−x2y)=−2xy−x2dydx
Setting the derivative of the left-hand side equal to the derivative of the right-hand side (which is 0 since 2a3 is a constant):
y2+2xydydx−2xy−x2dydx=0
Step 3: Rearranging the Derivative
Rearranging the equation, we have:
(2xy−x2)dydx+y2−2xy=0
Factoring out dydx:
dydx(2xy−x2)=2xy−y2
Thus, we can express dydx as:
dydx=2xy−y22xy−x2
Step 4: Set the Derivative to Zero
Setting dydx=0:
2xy−y2=0
Factoring gives:
y(2x−y)=0
This leads to two cases:
1. y=0
2. y=2x
Step 5: Analyze the Critical Points
1. Case 1: If y=0, substituting back into the original equation gives:
x⋅0⋅(0−x)=2a3⟹0=2a3
This is not valid since a is a constant.
2. Case 2: If y=2x, substituting into the original equation:
x(2x)2−x2(2x)=2a3
Simplifying:
4x3−2x3=2a3⟹2x3=2a3⟹x3=a3
Taking the cube root:
x=a
Step 6: Conclusion
Thus, we have shown that the value of the function xy(y−x)=2a3 is minimized at x=a.
The given function is:
xy(y−x)=2a3
Expanding this, we have:
xy2−x2y=2a3
To find the critical points, we need to differentiate the function with respect to x. We will apply the product rule for differentiation.
ddx(xy2)=y2+2xydydx
ddx(−x2y)=−2xy−x2dydx
Setting the derivative of the left-hand side equal to the derivative of the right-hand side (which is 0 since 2a3 is a constant):
y2+2xydydx−2xy−x2dydx=0
Rearranging the equation, we have:
(2xy−x2)dydx+y2−2xy=0
Factoring out dydx:
dydx(2xy−x2)=2xy−y2
Thus, we can express dydx as:
dydx=2xy−y22xy−x2
Setting dydx=0:
2xy−y2=0
Factoring gives:
y(2x−y)=0
This leads to two cases:
1. y=0
2. y=2x
1. Case 1: If y=0, substituting back into the original equation gives:
x⋅0⋅(0−x)=2a3⟹0=2a3
This is not valid since a is a constant.
x(2x)2−x2(2x)=2a3
Simplifying:
4x3−2x3=2a3⟹2x3=2a3⟹x3=a3
Taking the cube root:
x=a
Thus, we have shown that the value of the function xy(y−x)=2a3 is minimized at x=a.
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6g
23 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6h (multiple Choice Questions)
10 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6e
16 Videos
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise
19 Videos
Similar Questions
Knowledge Check
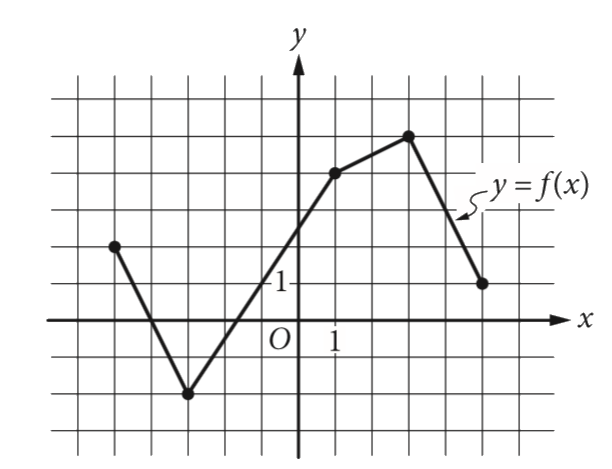
The complete graph of the function f is shown in the xy-plane above. For what value of x is the value of f(x) at its minimum?A−5B−3C−2D3
For what values of x, the function f(x)=x5−5x4+5x3−1 is maximum or minimum? Prove that at x = 0, the function is neither maximum nor minimum.
View SolutionIf the function x2−2kx+3 is minimum at x=3 then find the value of k.
View SolutionThe minimum value of the function y=|2x+1|+2|x−2|, is
View SolutionFind the maximum and minimum values of the function y=x3,inx∈[−2,3]?
View SolutionIf x+y=1 then find the maximum value of the function xy2
View SolutionIf the function y=aex+bx2+3x is maximum at x = 0 and minimum at x = - 3, then find the values of a and b.
View SolutionProve that the minimum value of 3cosx+4sinx+5 is 0.
View Solution
