Prove that the function f(x)=x2−x+1 is neither increasing nor decreasing on (−1, 1) .
f(x)=x2−x+1
⇒f'(x)=2x−1
Let f'(x)=0
⇒2x−1=0
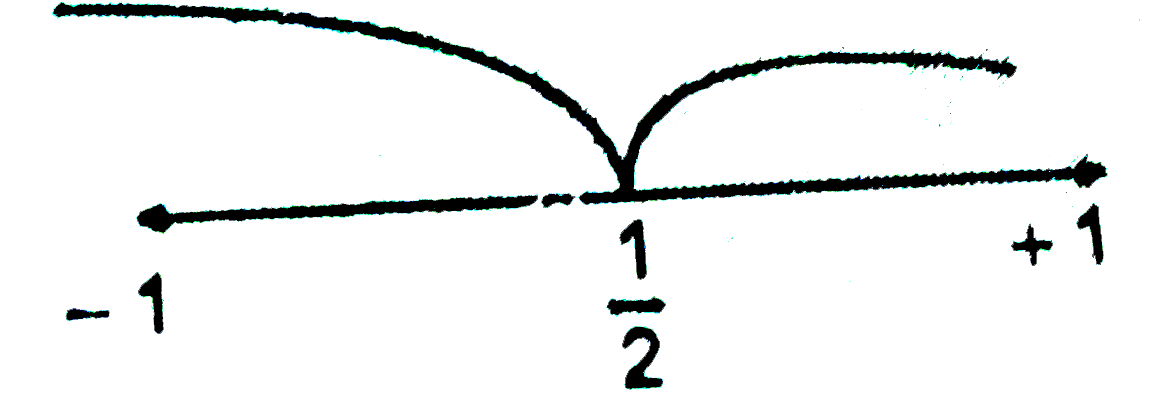
⇒x=12

∵ In (-1, 1), f'(x) has not same sign.
∴ f(x) is neither increasing nor decreasing in (-1, 1).
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6.3
27 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6.4
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6.1
18 Videos
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise
19 Videos
Similar Questions
Prove that the function f(x)=cosx is neither increasing nor decreasing in (0, 2π)
View SolutionProve that the function f defined by f(x)=x^2−x+1 is neither increasing nor decreasing in (−1,1). Hence find the intervals in which f(x) is strictly increasing and strictly decreasing.
View SolutionShow that the function x2−x+1 is neither increasing nor decreasing on (0, 1) .
View SolutionShow that the function f(x)=x2 is neither strictly increasing nor strictly decreasing on R .
View SolutionShow that f(x)=11+x2 is neither increasing nor decreasing on R .
View SolutionProve that the functionf(x)=2x−13x+4 is increasing for all x R.
View SolutionThe function f(x)=x2−x+1 is increasing and decreasing in the intervals
View SolutionThe function f(x)=log(1+x)−(2+x) is increasing in
View SolutionProve that the function f given by f(x)=x−[x] is increasing in (0, 1) .
View SolutionProve that the function f given by f(x)=x−[x] us increasing in (0,1).
View Solution
