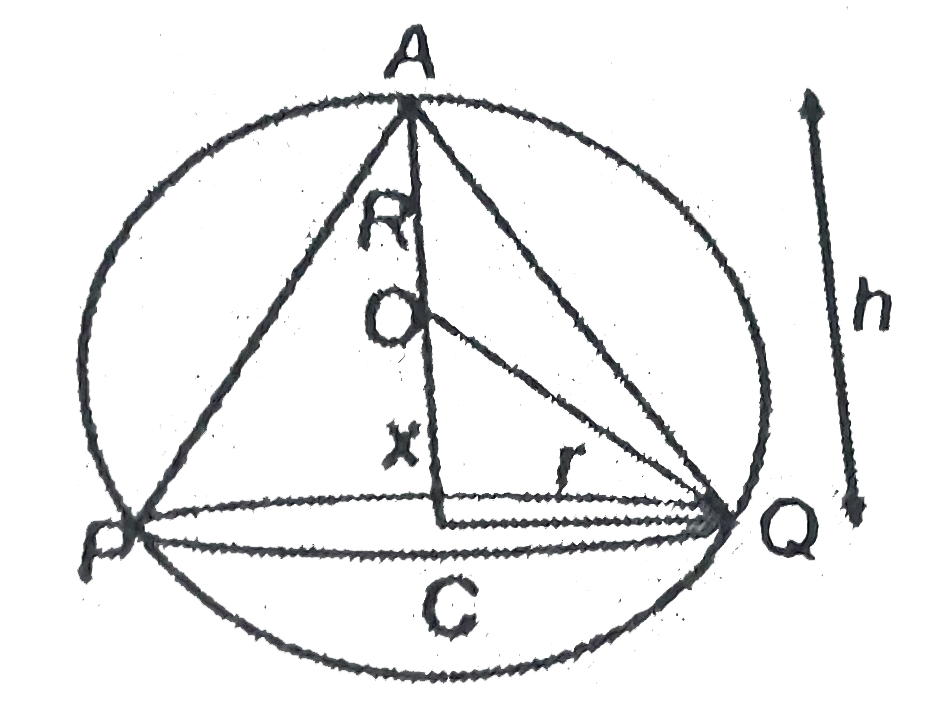
Prove that the volume of the largest cone, that can be inscribed in a sphere of radius $R .$ is $\frac{8}{27}$ of the volume of the sphere.

Video Solution

Text Solution

Verified by Experts

Let $O C = x, C Q = r$
Now OA=R (given)
height of cone = h = x + R …(1)
$∴ Volume of e = V = \frac{1}{3} π r^{2} h$
Now in right $Δ O C Q,$
$O C^{2} + C Q^{2} = C Q^{2}$
$\Rightarrow x^{2} + r^{2} = R^{2}$
$\Rightarrow r^{2} = R^{2} - x^{2}$ ....(2)
put the values of h and r from equations (1) and (2) in V,
$V = \frac{1}{3} π [(R^{2} - x^{2}) - 2 x (x + R)]$
Differentiate equation (3) w.r.t. x,
$\frac{d V}{d x} = \frac{1}{3} π [R^{2} - x^{2}) - 2 x (x + R)]$
$\Rightarrow \frac{d V}{d x} = \frac{π}{3} [R^{2} - x^{2} - 2 x^{2} - 2 x R]$
$\Rightarrow \frac{d V}{d x} = \frac{π}{3} (R^{2} - 2 x R - 3 x^{2})$
$\Rightarrow \frac{d V}{d x} = \frac{π}{3} (R - 3 x) (R + x)$ ....(4)
For maximum value $\frac{d V}{d x} = 0$
$\Rightarrow \frac{π}{3} (R - 3 x) (R + x) = 0$
$\Rightarrow x = \frac{R}{3} p r x = - R \Rightarrow x = \frac{R}{3}$
$(. ∵$ x cannot be negative)
Differentiate equation (4) w.r.t. x,
$\frac{d^{2} V}{{d x}^{2}} = \frac{π}{3} [(- 3) (R + x) + (R - 3 x)]$
$\frac{π}{3} (- 2 R - 6 x) = - \frac{π}{3} (2 R + 6 x)$
at $x = \frac{R}{3}, \frac{d^{2} V}{d r^{2}} = \frac{- π}{3} (2 R + \frac{6 R}{3}) = - \frac{4 π}{3} R < 0$
$∴ local maximum value of V is at x = \frac{R}{3}$ .
Now, put the value of x in equation (3),
$V = \frac{π}{3} (R^{2} - \frac{R^{2}}{9}) (R + \frac{R}{3})$
$\frac{π}{3} \cdot \frac{8 R^{2}}{9} \cdot \frac{4 R}{3} = \frac{8}{27} (\frac{4}{3} π R^{3})$
$\Rightarrow V = \frac{8}{27} \times$ Volume of sphare .

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF DERIVATIVES-Exercise 6.5

Home
Ask Doubt
Profile