A random variable x has its range {0,1,2} and the probabilities are given by P(x=0)=3k3,P(x=1)=4k−10k2,P(x=2)=5k−1 where k is a constant then k=
Step by step video & image solution for A random variable x has its range {0,1,2} and the probabilities are given by P(x=0) =3k^(3), P(x=1) =4k-10k^(2) , P(x=2) =5k-1 where k is a constant then k= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
The p.m.f. of a r.v. X is as follows :
P(X=0)=3k3,P(X=1)=4k−10k2,P(X=2)=5k−1,
P(X=x)=0 for any other values of x, then k =A1B2C3D13 - Question 2 - Select One
The p.m.f. of a r.v. X is as follows :
P(X=0)=3k3,P(X=1)=4k−10k2,P(X=2)=5k−1,
P(X=x)=0 for any other values of x, then P(0<X<3) =A19B89C23D13 - Question 3 - Select One
The p.m.f. of a r.v. X is as follows :
P(X=0)=3k3,P(X=1)=4k−10k2,P(X=2)=5k−1,
P(X=x)=0 for any other values of x, then P(X<1)=A19B89C23D13
A random variable X has the following probability distribution:
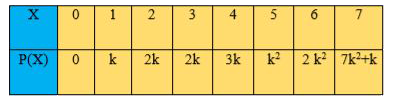
Determine : (i) k (ii) P(X<3) (iii) P(X>4)View SolutionIf a random variable "X" takes values (−1)k2kk,k=1,2,3,... with probabilities P(X=k)=12k, then E(X)
View SolutionThe p.m.f. of a.r.v. X is as follows:
P(X=0)=3k3,P(X=1)=4k−10k2, P(X=2)=5k-1, P(X=x)=0 for any other value of x, then value of k isView SolutionA random variable X takes the values 0,1,2,3,..., with prbability PX(=x)=k(x+1)(15)x, where k is a constant, then P(X=0) is.
View SolutionThe probability distribution of random variable X with two missing probabilities p1 and p2 is given below
XP(X)1k2p134k4p252k
It is further given that P(X≤2)=0.25andP(X≥4)=0.35. Consider the following statements
1. p1=p2
2. p1+p2=P(X=3)
which of the statements given above is/are correct ?View Solution
