In Fig. 4, a sector OAP of a circle with centre O, containing ∠0. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r.
[tan 0 + sec 0 + π0180∘−1]
![In Fig. 4, a sector OAP of a circle with centre O, containing angle0. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r. [tan 0 + sec 0 + (pi0)/(180^(circ)) -1]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/VKP_XAM_IDA_MAT_X_MQP_02_E01_032_Q01.png)
The correct Answer is:[Hint: Perimeter of shaded region = AB + PB + AP, =r tanθ+rsecθ−r+πrθ180]
Step by step video, text & image solution for In Fig. 4, a sector OAP of a circle with centre O, containing angle0. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r. [tan 0 + sec 0 + (pi0)/(180^(circ)) -1] by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER -2 [UNSOLVED]EXERCISE - SECTION-C11videos
MODEL QUESTION PAPER -2 [UNSOLVED]
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER - 9 [UNSOLVED]EXERCISE - SECTION - D7videos
MODEL QUESTION PAPER - 9 [UNSOLVED]
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER -7 EXERCISE - SECTION -D8videos
MODEL QUESTION PAPER -7
Similar Questions
In the given figure, is shown a sector OAP of a circle with centre 0, containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r[tanθ+secθ+πθ180−1]
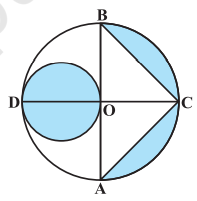
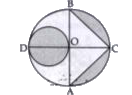
View SolutionIn Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA=7 cm, find the area of the shaded region
View Solution
Knowledge Check
- Question 1 - Select One
AB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
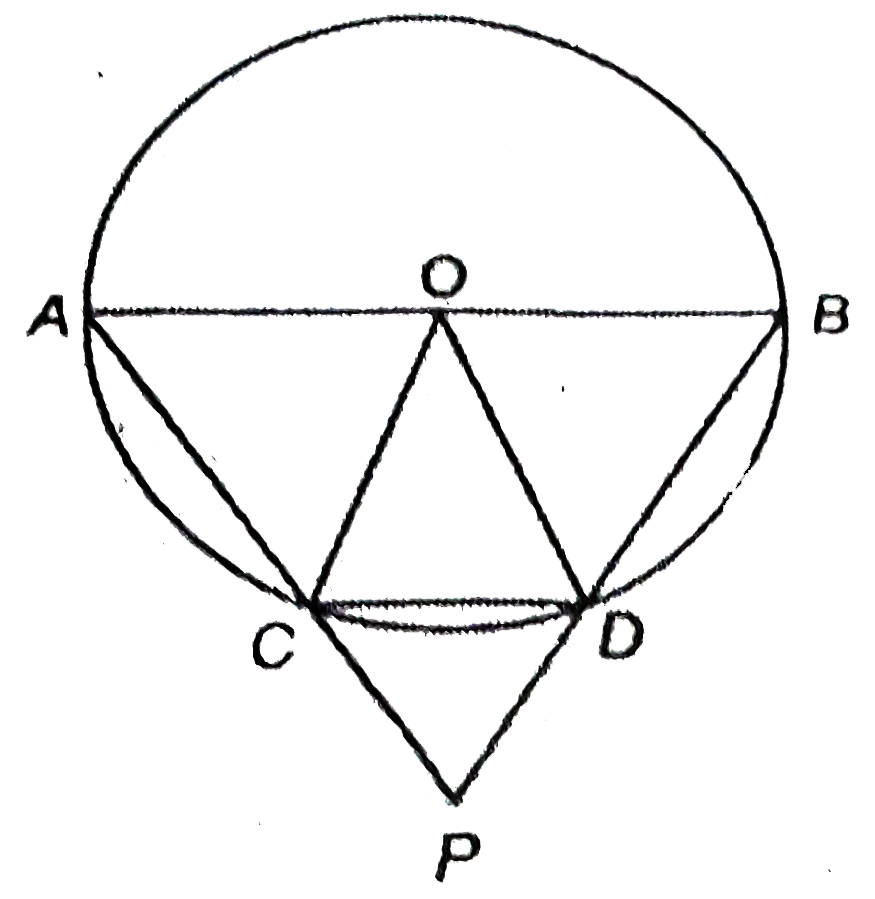A60∘B30∘C90∘D160∘
Figure shows a sector of a circle, centre O, containing an angle θ. Prove that (i) Perimeter of the shaded region is r(tanθ+secθ+πθ180−1) (ii) Area of shaded region is r22(tanθ−πθ180)
View SolutionIf Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.
View SolutionFig. 15.17, shows a sector of a circle, centre O , containing an angle θo , prove that: (FIGURE) (i) Perimeter of the shaded region is r (tanθ+secθ+πθ180−1) (ii) Area of the shaded region is r22 (tanθ−πθ180)
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.
View SolutionIn the given figure, AB and CD are two diameters of a circle (with centre 0) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
View SolutionFigure shows a sector of a circle of radius r containing an angle θ∘ The area of the sector is Acm2 and the perimeter is 50cm. Prove that θ=360π(25r−1) and A=25r−r2
View SolutionThe median AD of a ΔABC is perpendicular to AB, prove that tanA+2tanB=0
View Solution