In Figure point T is the interior of reactangle PQRS, Prove that, TS2+TQ2+TR2 (As shown in the figure, drawn seg AB || side SR and A-T-B)
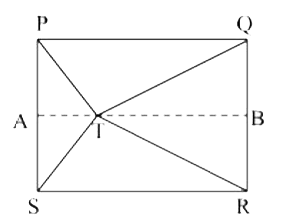
The correct Answer is:TS2+TQ2=TP2+TR2
Topper's Solved these Questions
- PYTHAGORS THEORMBOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - PROBLEM SET 2
30 Videos
- PYTHAGORS THEORMBOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - HOTS-SOLVED
5 Videos
- PYTHAGORS THEORMBOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - HOTS
1 Videos
- PROBABILITY BOOK - UNIQUE PUBLICATIONCHAPTER - PROBABILITY EXERCISE - PROBLEM SET 5
23 Videos
- QUADRATIC EQUATIONS BOOK - UNIQUE PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNMENT
6 Videos
Similar Questions
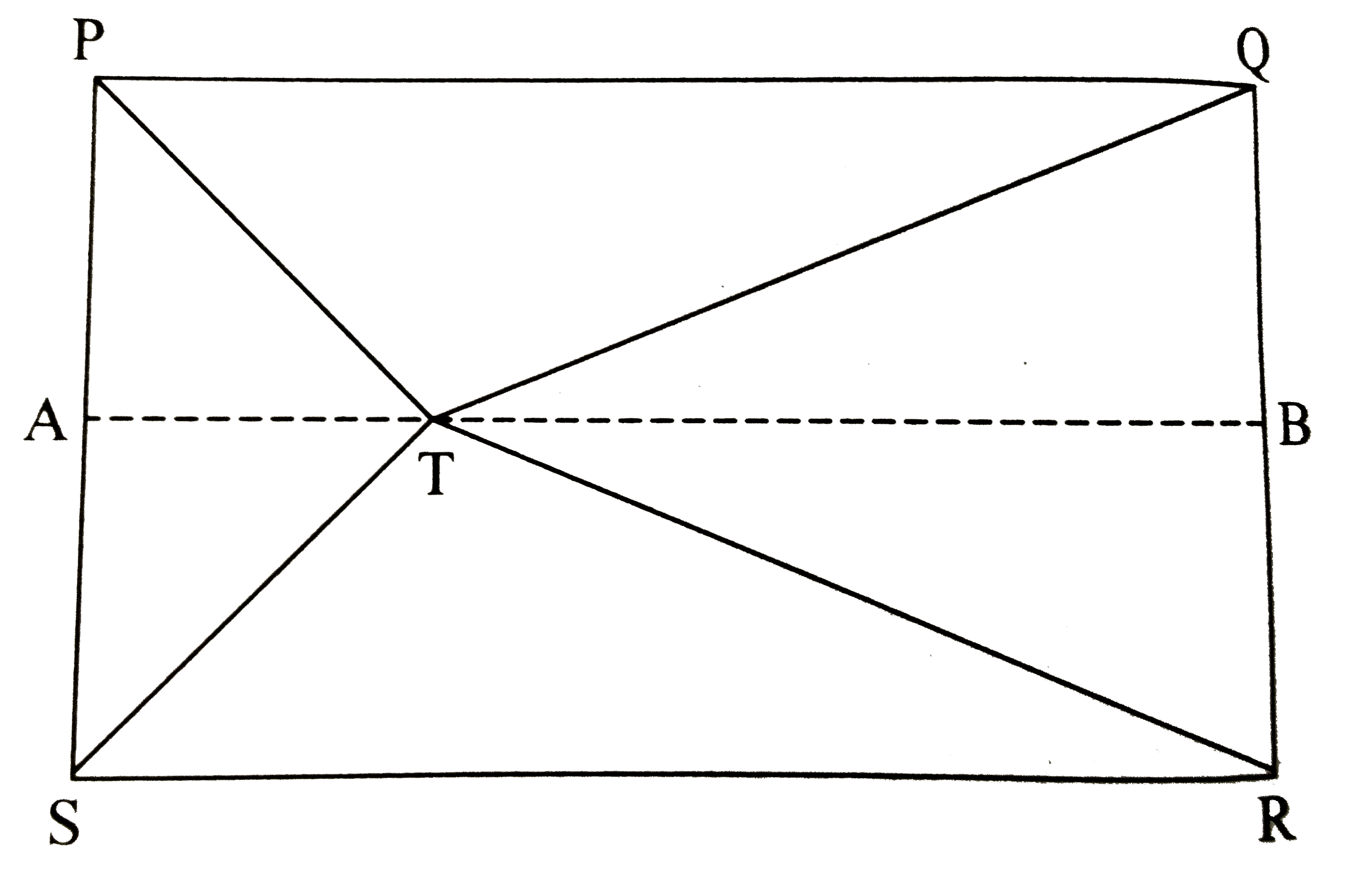
In the figure , point T is in the interior of rectangle PQRS.
Prove that,
TS2+TQ2=TP2+TR2
(As shown in the figure, draw seg AB∣∣ side SR and A−T−B.)
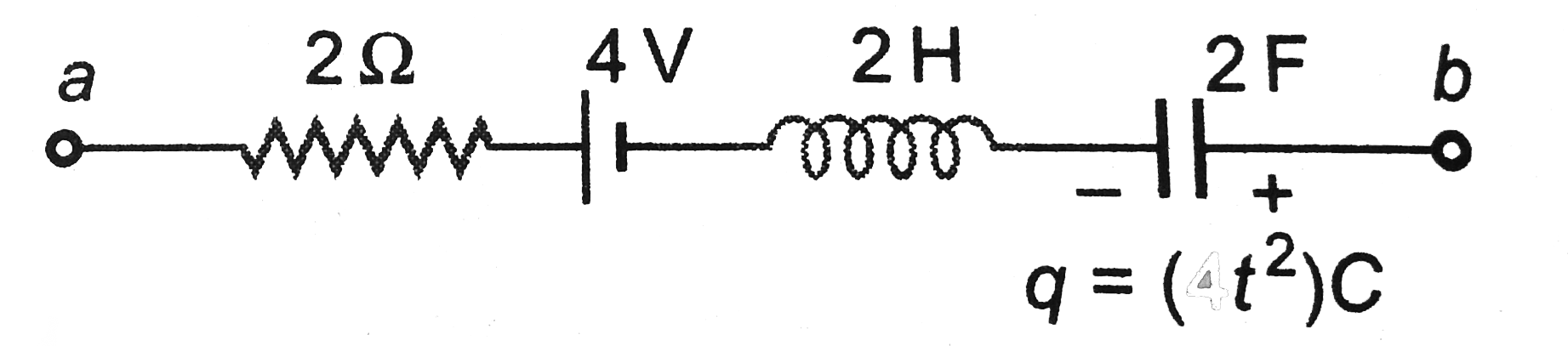
View SolutionIn the figure shown Vab at t=1 is
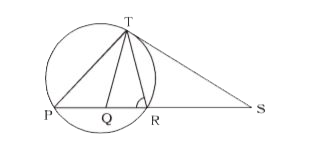
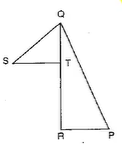
View SolutionIn figure below, TS is the tangent at T and TQ the bisector of ∠PTR. Then TS is equal to:
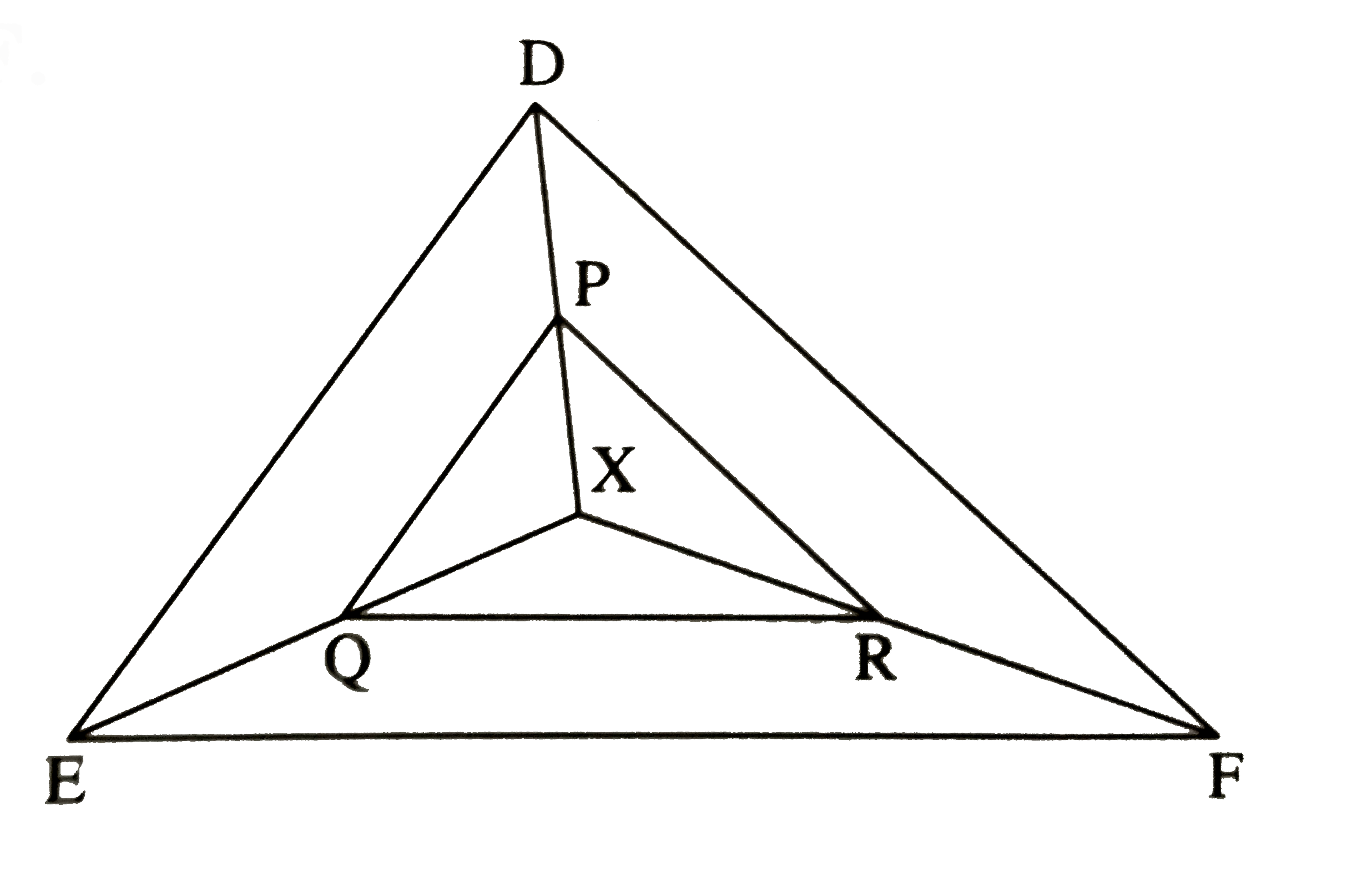
View SolutionIn the figure X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ∣∣ set DE, set QR∣∣ set EF. Fill in the blanks to prove that set PR∣∣ seg DF.
View SolutionIn Figure, T is a point on side QR of PQR and S is a point such that RT=ST. Prove That : PQ+PR>QS
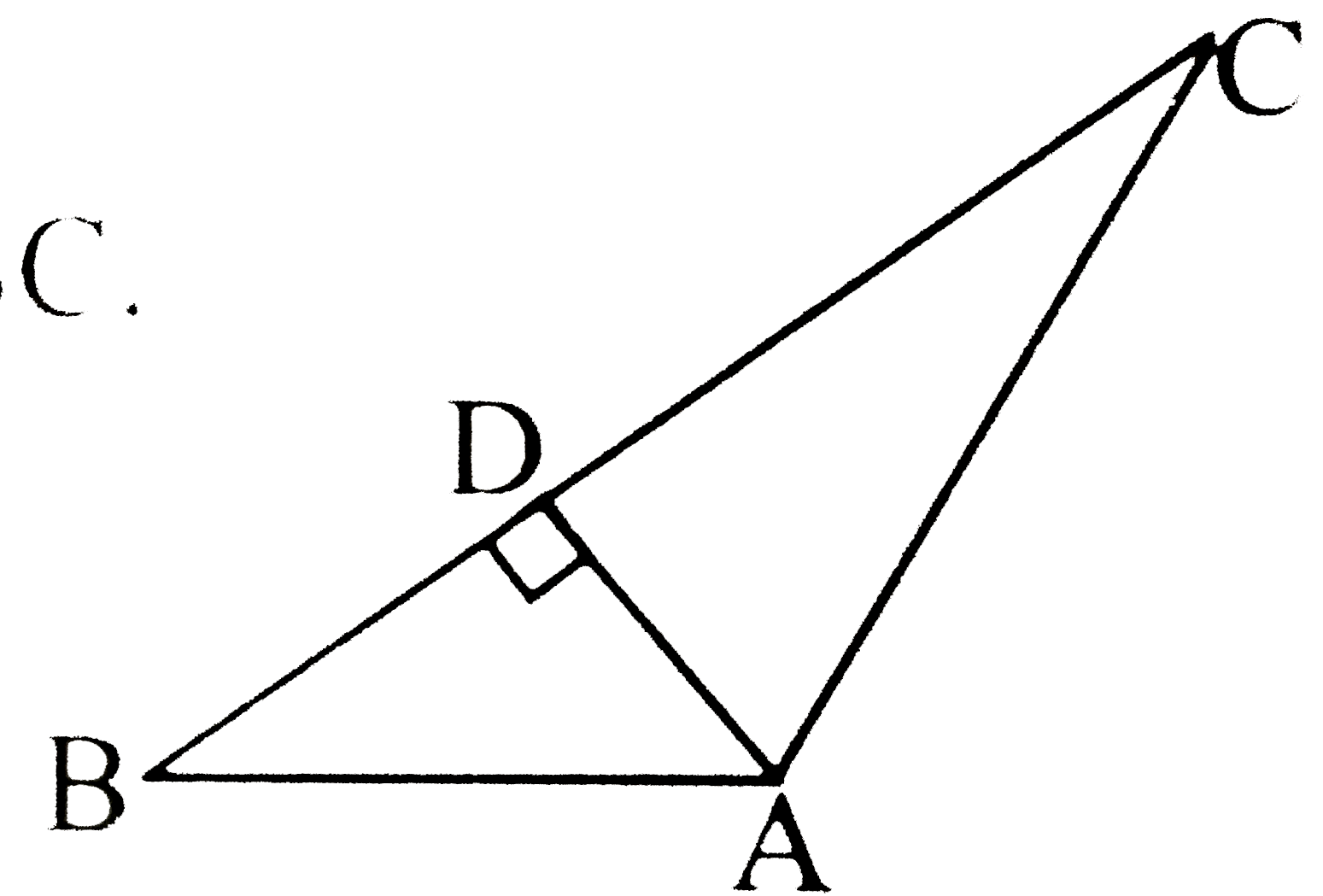
View SolutionSee the given figure. In ΔABC, seg AD⊥ seg BC. Prove that: AB2+CD2=BD2+AC2
View SolutionIn the adjoining figure, P is an interior point of ΔABC. Then prove that :
AB+BC+CA<2(PA+PB+PC)

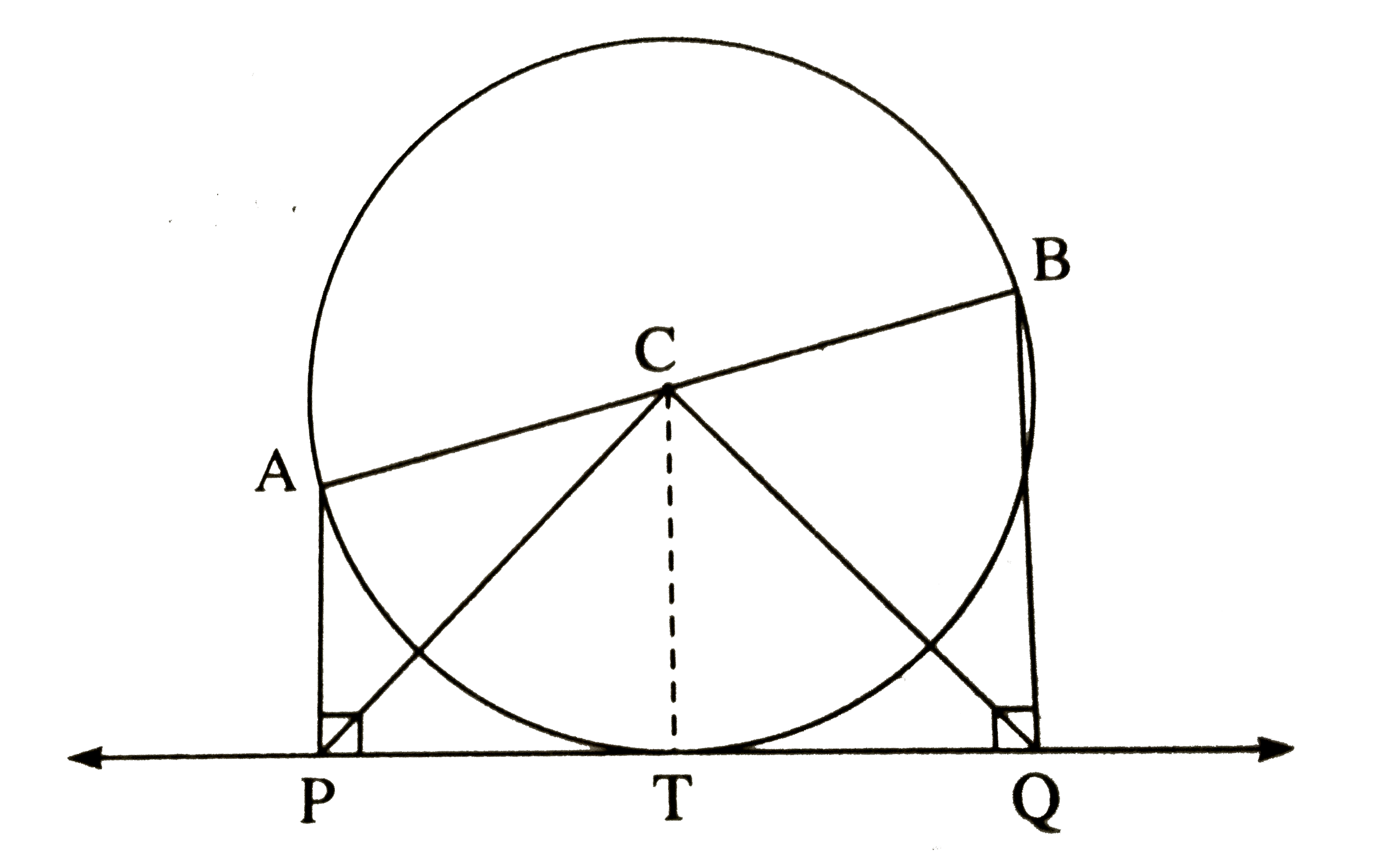
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
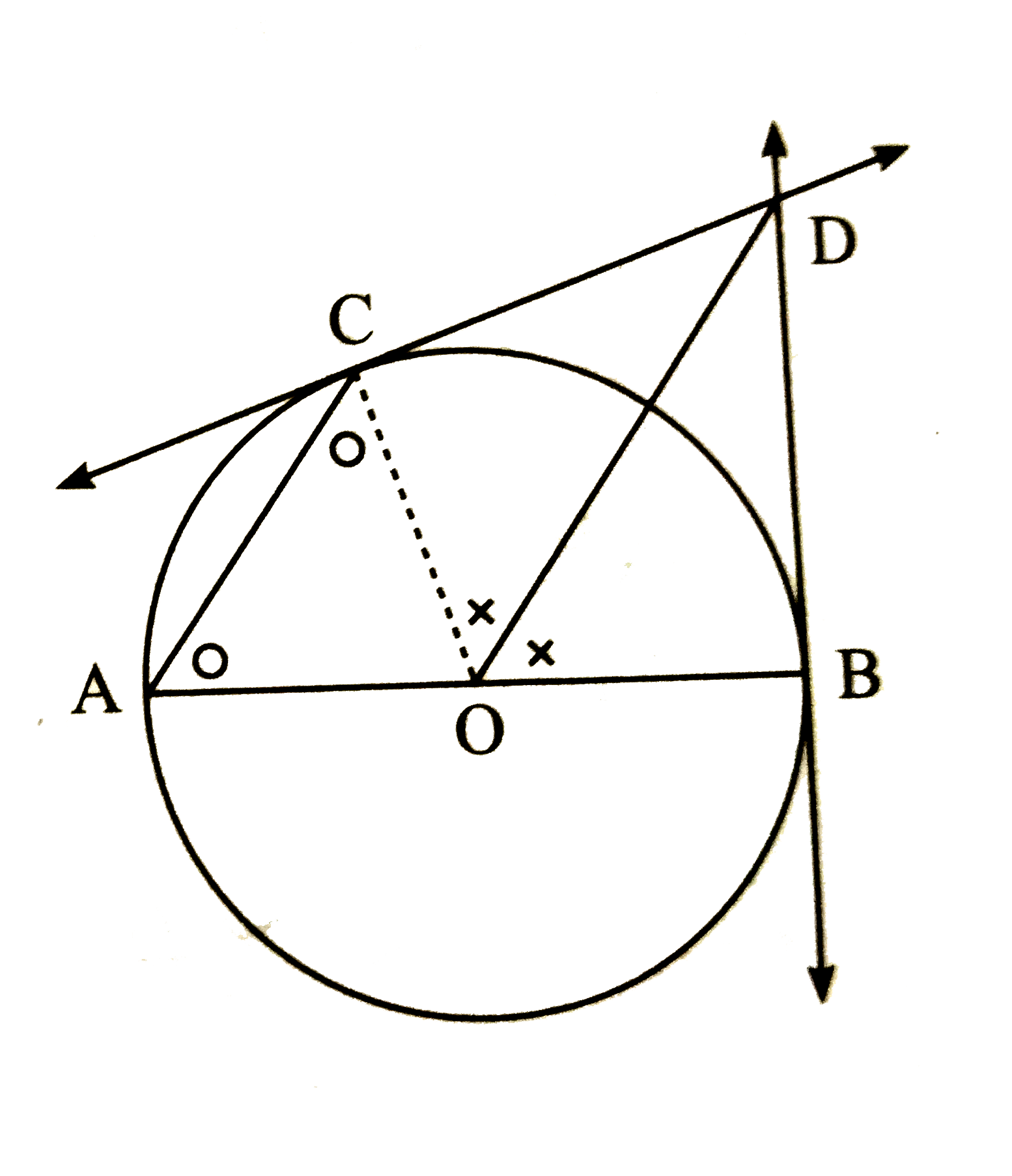
View Solution
