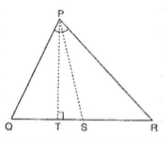
In adjoining figure, seg PS is the median of ΔPQRadnPT⊥QR. Prove that
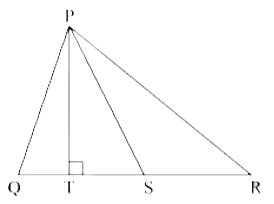
(1) PR2=PS2+QR×ST+(OR2)2
(2) PQ2=PS2+QR×ST+(QR2)2
Text Solution
The correct Answer is:BC=18 cm
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - PROBLEM SET 230videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - HOTS-SOLVED5videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - HOTS1videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PROBABILITY EXERCISE - PROBLEM SET 523videos
PROBABILITY
- BOOK - UNIQUE PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNMENT6videos
QUADRATIC EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔPQR, Ps is the bisector of <P and PT⊥QR, then <TPS is equal to
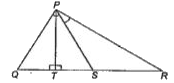 A<Q+<RB90∘+12<QC90∘−12<RD12(<Q−<R)
A<Q+<RB90∘+12<QC90∘−12<RD12(<Q−<R) - Question 2 - Select One
In Δ PQR,PS is the bisector of ∠PandPT⊥QR, where ∠ Q = 60 and ∠R = 30 then ∠TPS is equal to
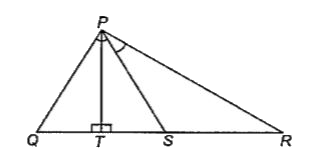 A10B30C60D15
A10B30C60D15
If S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View SolutionIn the given figure, seg PM is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.
 View Solution
View SolutionSeg Pm is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.
View SolutionIn the adjoining figure, ΔPQR is an equilateral triangle. Point S is on seg QR. such that QS=13QR. Prove that : 9PS2=7PQ2.
View SolutionIn the adjoining figure , if PQ=6,QR=10,PS=8 , find TS.
 View Solution
View SolutionIn Figure PS is the bisector of ∠QPR and PT⊥QR . Show that ∠TPS=12(∠Q−∠R).
 View Solution
View Solution

