Observe the picture and answer the following questions.
a. What is an ellipse?
b. What are the points $F_{1} and F_{2}$ called?
c. Give one property of an ellipse.

Text Solution

Verified by Experts

a. An ellipse is a curve obtained when a cone is cut by an inclined plane. Mathematically ellipse is defined as the sum of the distance to the two focal points from every point on the curve is constant.
b. The points $F_{1} and F_{2}$ are called foci or Focal points of the ellipse.
c. The sum of the distance to the two focal points from every point on the curve is constant. If A, B, C are any three points on the curve (ellipse) then, $A F_{1} + A F_{2} = B F_{1} + B F_{2} = C F_{1} + C F_{2}$

|

Updated on:21/07/2023

Class 10 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Observe these compounds and give answer of following question :

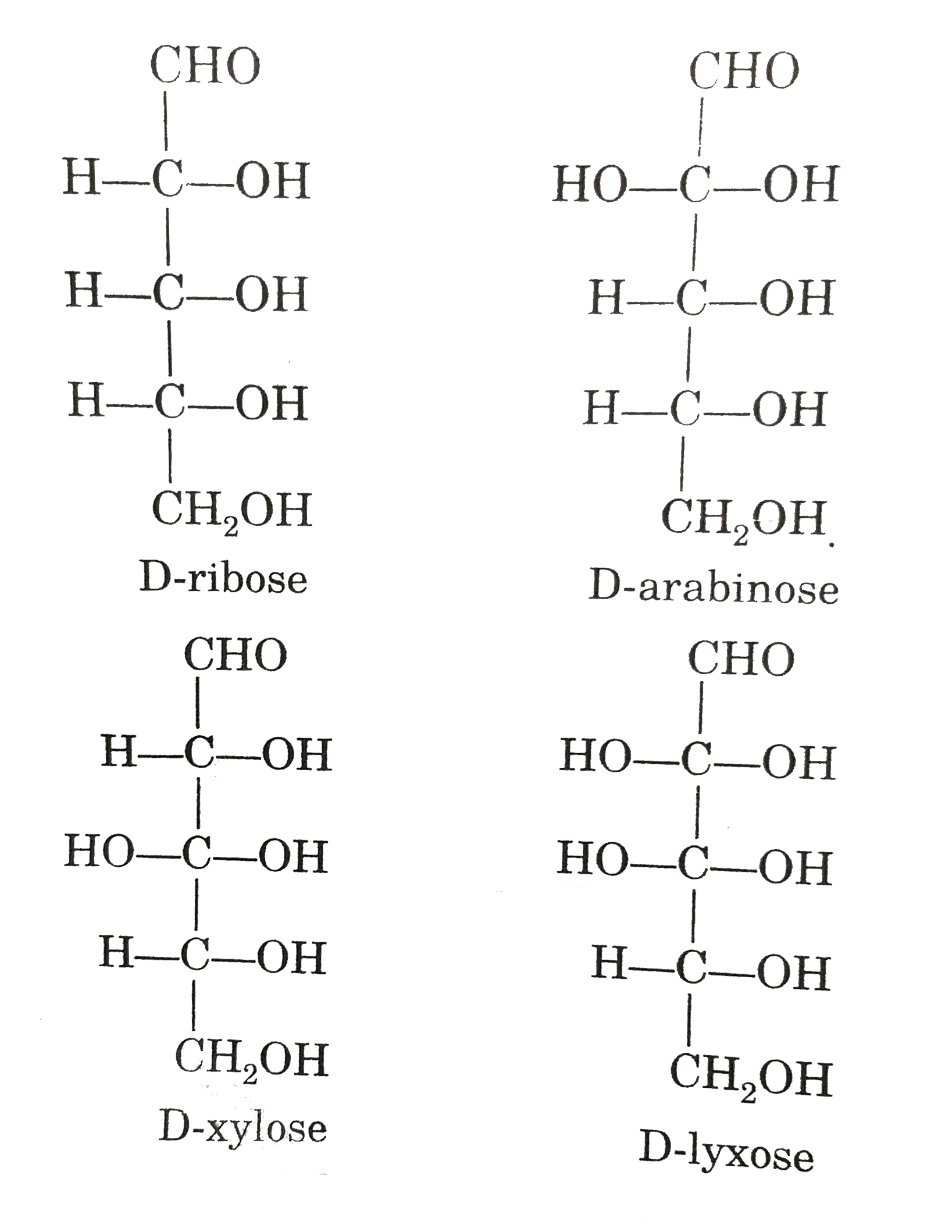
What is the relationship betweenC-5-epimer of D-tolose and C-2-epimer of D-talose and C-2-epimer ofC-3-epimer of F-mannose
Aenantiomer
Bdiastereic isomer
Cidential
Danomer
Question 2 - Select One
If the circle whose diameter is the major axis of the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ meets the minor axis at point P and the orthocentre of $Δ P F_{1} F_{2}$ lies on the ellipse, where $F_{1} and F_{2}$ are foci of the ellipse, then the square of the eccentricity of the ellipse is
A $\frac{\sqrt{5} - 1}{2}$
B $\sqrt{3} - 1$
C $\frac{1}{\sqrt{2}}$
D $\frac{\sqrt{3}}{2}$
Question 3 - Select One
Let $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1, a > b$ , be an ellipse with foci $F_{1}$ and $F_{2}$ . Let AO be its semi-minor axis. Where O is the centre of the ellipse. The lines $A F_{1}$ and $A F_{2}$ , when extended, , cut the ellipse again at point B and C respectively. Suppose that the triangle ABC is equilateral. Then the eccentricity of the ellipse is
A $\frac{1}{\sqrt{2}}$
B $\frac{1}{\sqrt{3}}$
C $\frac{1}{3}$
D $\frac{1}{2}$

UNIQUE PUBLICATION-GRAVITATION-ACTIVITY QUESTIONS

Home
Ask Doubt
Profile