A metal rod of length 1m rotates about an end with a uniform angular velocity $π / 3 r a d / s$ . A uniform magnetic field of 0.01 T exists in the region in a direction parallel to the axis of rotation. Calculate the emf induced between the ends of the rod.

Text Solution

Verified by Experts

As shown in the figure, rod PQ of length l (say) rotates about P with angular speed $ω$ (say) in the plane of the diagram. The magnetic field is perpendicular to the plane of the diagram downwards. Consider an element of length dx on the rod at a distance x from P.

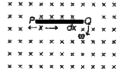
The linear speed of element of length l, $v = ω x$ . As, it moves perpendicular to its length and also perpendicular to the magnetic field, it cuts magnetic flux at the rate Bv dx,
i.e. $\frac{d ϕ}{d t} = B v d x$
$∴$ Magnitude of induced emf between the ends of element = de = Bvdx = $B ω d x$
$∴$ Net induced emf between ends of rod is
$e = \int_{0}^{e} d e = \int_{0}^{1} B ω x d x = \frac{1}{2} B ω l^{2}$
Given, $l = 1 m, ω = \frac{π}{3} r a d / s and B = 0.01 T$
$∴ e = \frac{1}{2} B ω l^{2} = \frac{1}{2} \times 0.01 \times \frac{π}{3} \times 1^{2} = 5.24 \times 10^{- 3} V$

Updated on:21/07/2023