A metal rod length l rotates about on end with a uniform angular velocity . A uniform magnetic field exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they money in circular paths.
Consider an element dx of the rod at a distance x from the axis of rotation
The linear speed of this element is
The element moves in a direction perpendicular to its length as well as perpendicular to the magnetic field
The emf induced between the ends of this element is
The emfs of all such elements will add to give the net emf between the ends of the rod
This emf is, therefore, .
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Short Answer
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 1
12 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
(a) A metal rod of length L rotates about an end with a uniform angular velocity ω . A uniform magnetic field B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they move in circular paths.
(b) A rod of length L rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. Find the potential difference (i) between the centre of rod and one end and (ii) between the two ends of the rod.
View SolutionA metal rod of length 15×10−2m rotates about an axis passing through one end with a uniform angular velocity of 60 rad s−1. A uniform magnetic field of 0.1 Tesla exisits in the direction of the axis of rotationn. Calculate the EMF induced between the ends of the rod.
View Solution
Knowledge Check
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ωA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
AzeroB12ωBI2CωBI2D2ωBI2A conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
 ABωl2B12Bωl2C18Bωl2Dzero
ABωl2B12Bωl2C18Bωl2Dzero
A rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA copper rod AB of length l is rotated about one end A with a constant angular velocity ω. Calculate the electric field at a distance x from the axis of rotation. Also determine PD between A and B.
View SolutionA copper rod of length l rotates an angular velocity ω in a uniform magnetic field B as show in figure . What is the induced emf across its ends ?
View SolutionA conducting rod of length 2l is rotating with constant angular speed ω about is perpendicular bisector. A uniform magnetic field →B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
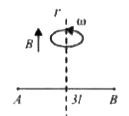
View SolutionA copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
View Solution
