Find an expression for emf induced in a coil rotating with uniform speed in a uniform magnetic field.

Text Solution

Verified by Experts

Consider a coil ABCD rotating about an XY-axis in between the two pole pieces of a magnet. When plane of the coil is parallel to the direction of lines of force, no line of force cuts through it. Thus, the magnetic flux linked with the coil is minimum.
If the coil is perpendicular to the direction of lines of force, maximum lines cut through it. Thus, magnetic flux linked with it is maximum.
Now, if the coil rotates with uniform velocity, the flux linked with it undergoes a continuous change between minimum and maximum. Due to this continuous change of magnetic flux, an emf is induced in the coil. Let AD be the instantaenous position of the coil. Let AD be the instantaneous position of the coil. Time is measured from the instant coil perpendicular to the lines. If $θ$ turned by the coil is given by
$θ = ω t$
where, $ω$ is the angular velocity of the coil
The magnetic flux linked with the coil is given by
$ϕ = N A B$
where, A is the cross-sectional area, N is the number of turns of coil and B is the magnetic field between two poles.

From $Δ A E C, \frac{C E}{A C} = cos θ$
$\Rightarrow \frac{A^{.}}{A} = cos ω t$
$\Rightarrow A^{.} = A cos ω t$
where, A is the actual area of coil.
$∴ ϕ = N B A cos ω t$
This is the value of instantaneous magnetic flux linked with the coil.
Differentiating both sides w.r.t. t, we get
$\frac{d ϕ}{d t} = \frac{d}{d t} (N A B cos ω t)$
$= N A B \frac{d}{d t} (cos ω t)$
$\frac{d ϕ}{d t} = N A B ω sin ω t$
According to Faraday.s law of electromagnetic induction,
$e = \frac{- d ϕ}{d t}$
$\Rightarrow e = N A B ω sin ω t$
$e = e_{0} sin ω t [∵ e_{0} = N A B ω]$
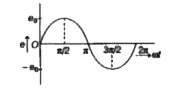
At $ω t = 0, e = 0$
At $ω t = \frac{π}{2}, e = e_{0} and At ω t = π, e = 0$
At $ω t = \frac{3 π}{2}, e = - e_{0} and At ω t = 2 π, e = 0$
The graph between e and $ω t$ is shown as below

Updated on:21/07/2023

An emf induced in a coil rotating in a uniform magnetic field is given by
A $e = e_{0} sin ω t$
B $e_{0} = e sin ω t$
C $e = sin ω t$
D $e = e_{0} sin ω$
The maximum value of emf indued in a coil rotating in a uniform magnetic field is called as
Apeak emf
Brms emf
CD.C. emf
Dall of these
The phase difference between the flux linkage and the induced e.m.f. in a rotating coil in a uniform magnetic field
A $π$
B $π / 2$
C $π / 4$
D $π / 6$