Derive the expression for motional emf induced in a conductor moving in a uniform magnetic field.

Video Solution

Text Solution

Verified by Experts

Consider a conducting coil of N turns and area A rotating with a uniform angular velocity $\to ω$ about an axis in the plane of the coil, and perpendicular to a uniform magnetic field of induction $\to B$ , as shown in Fig 1. The frequency of rotation of the coil is $f = ω / 2 π .$

Suppose that a time t = 0, the coil is in position PQ, with its plane perpendicular to the magnetic field. In time t, the coil rotates through an angle $θ$ to position P'Q'.
In this position, the normal to the plane of the coil makes an angle $θ (= ω t)$ with the mgnetic field and the magnetic flux through the coil is ltbr> $Φ = N \to B \cdot \to A = N B A cos θ = N B A cos ω t$
As the coil rotates, the changing magnetic flux induces an emf in the coil given by
$E = - \frac{d Φ}{d t}$
$= - \frac{d t}{d t} (N B A cos ω t) = - N B A \frac{d}{d t} (cos ω t) = N B A ω sin ω t$
$∴ E = E_{0} sin ω t$ ,
where $E_{0} = N B A ω .$

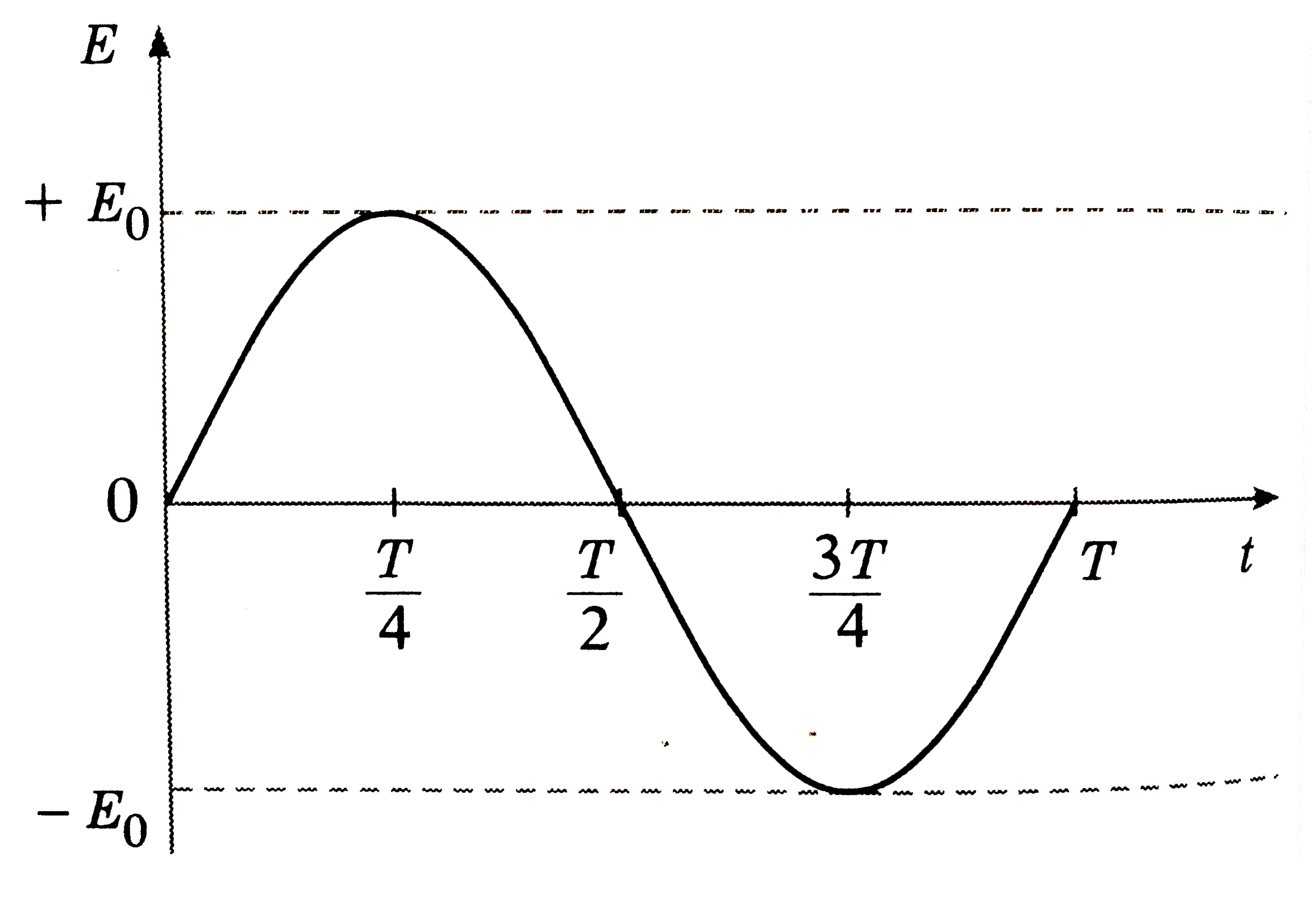
The induced emf varies as $sin ω t$ and is, therefore, called sinusoidally alternating emf. In one rotation of the coil, $sin ω t$ varies between +1 and -1 and hence the induced emf varies between $+ E_{0} and - E_{0}$ . The maximum value $E_{0}$ of an alternating emf is called the peak value or emplitude of the emf.
The sinusoidal variation of the emf with time over cycle is shown in Fig. 2. $T (= \frac{1}{f})$ is the period of the emf, which is the same as the period of rotation of the coil. The emf changes direction at the end of every half rotation of the coil, i.e. after time $\frac{T}{2} .$
[Note : For the graph of E against $θ$ , change the labelling $t \to θ, \frac{T}{4} \to π / 2, \frac{T}{2} \to π, \frac{3 T}{4} \to 3 π / 2 and T \to 2 π$ on the x-axis.]

Updated on:21/07/2023

An emf induced in a coil rotating in a uniform magnetic field is given by
A $e = e_{0} sin ω t$
B $e_{0} = e sin ω t$
C $e = sin ω t$
D $e = e_{0} sin ω$
A particle is moving in a uniform magnetic field, then
AIts momentum changes but total energy remains the same
BBoth momentum and total energy remain the same
CBoth will change
DTotal energy changes but momentum remains the same
The phase difference between the flux linkage and the induced e.m.f. in a rotating coil in a uniform magnetic field
A $π$
B $π / 2$
C $π / 4$
D $π / 6$