An AC circuit contains a source of instantaneous emf E=E0sinωt and a capacitor of capacitance C. Derive an expression for the instantaneous current in it.
Let us consider a capacitor with capacitance C be connected to an AC source with emf having instantaneous value.
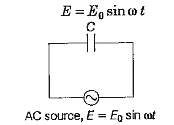
Due to the emf, charge will be produced and it will charge the plates of capacitor with positive and negative charge. If potential difference across the plates of capacitor is V, then
V=qC.orq=CV
The instantaneous value of current in the circuit,
I=dqdt=ddt(CE) [∴V=E]
=ddt(CE0sinωt) [∴E=E0sinωt]
=CE0cosωt×ω=CE0cosωt×ω
ωCE0cosωt=E01/ωCcosωt
[∴cosωt=sin(π/2+ωt)]
I=E01/ωCsin(ωt+π/2)
I will be maximum when sin(ωt+π2)=1
So, Imax=E01ωC=I0
∴I=I0sin(ωt+π⋅2)
From Eqs. (i) and (iii), it is clear that in perfect capacitor, the current leads the voltage by a phase angle of π/290∘ or the voltage lags behind the current by a phase angle π/2(90∘).
Similar Questions
In the given A.C. circuit, the instantaneous current through inductor and capacitor are 0.8 A and 0.4 A repectively. The instantaneous current through resistor is

View SolutionA capacitor of capacitance 2 μF is connected to an osillator giving an output voltage e = 20 sin ω t volt . If ω=10π rad/ s write an equation for instantaneous current through the circuit .
View Solution
Knowledge Check
Let f = 50 Hz, and C = 100 μF in an AC circuit containing a capacitor only. If the peak value of the current in the circuit is 1.57 A at t = 0. The expression for the instantaneous voltage across the capacitor will be
AC=50sin(100πt−π/2)BC=100sin(50πt)CC=50sin100πtDC=50sin(100πt+π/2)An a.c. emf of e=220 sin ω t is applied across the capacitor, the power consumption is
A0B55 WC110 WD220 WAn AC source producing emf V=V0 "["sin omega t+sin 2omegat"]" is connected in series with a capacitor and a resistor. The current found in the circuit is
Ai1−i2Bi1<i2Ci1>i2Di1 may be less than, equal to or greater than i2
A capactior of 1μF is connected ot an a.c. source of e.m.f E=250sin100πt. Write an equation for instantaneous current through the circuit and given reading of a.c. ammeter connected in the circuit.
View SolutionConsider the circuit shown in figure. The oscillating source of emf deliver a sinusoidal emf of amplitude emax and frequency ω to the inductor L and two capacitors C1 to C2. Find the maximum instantaneous current in each capacitor.
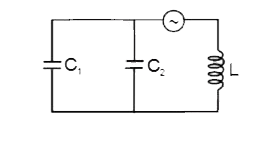
View SolutionAn emf E=100sin314tV is applied across a pure capacitor of 637(μ)F. Find
(a) the instantaneous current I
(b) the instantaneous power p.
View SolutionA capacitor of capacitive reactance 5ω is connected with A.C. source having voltage V=3sin(ωt+π/6). Find rms and Peak voltage rms and peak current and instantaneous current

View SolutionIn a.c. circuit, the instantaneous value of e.m.f. and current are
View Solution
