Establish the following Lens Maker’s formula.
1f=(μ−1)(1R1−1R2)
Lens maker .s formula
Similar Questions
Statement-1 : A glass convex lens (refractive index, μ1=1.5), when immersed in a liquid of refractive index μ2=2, functions as a diverging lens.
Statement-2 : The focal length of a lens is given by 1f=(μ−1)(1R1−1R2), where μ is the relative refractive index of the material of the lens with respect to the surrounding medium.
View SolutionStatement-1 : A glass convex lens (refractive index, μ1=1.5), when immersed in a liquid of refractive index μ2=2, functions as a diverging lens.
Statement-2 : The focal length of a lens is given by 1f=(μ−1)(1R1−1R2), where μ is the relative refractive index of the material of the lens with respect to the surrounding medium.
View Solution
Knowledge Check
Statement-1 : Focal length of an equiconvex lens of μ=3/2 is equal to radius of curvature of each surface.
Statement-2 : it follows from
1f=(μ−1)(1R1−1R2)AStatement-1 is true, Statement-2 is true.
Statement-2 is correct explanation of Statement-1.BStatement-1 is true, Statement-2 is true, but Statement-2 is not a correct explanation of Statement-1.CStatement-1 is true, Statement-2 is false.DStatement-1 is fasle, Statement-2 is true.STATEMENT-1 Power of a lens depends on nature of material of lens, medium in which it is placed and radii of curvature of its surface.
STATEMENT2 it follows the relationp=1f=(μ2μ1−1)[1R1−1R2]ASTATEMENT -1is true statement 2 is true,Statement -2is a correct explanation for statement -1BSTATEMENT -1is true statement 2 is true,Statement -2is a not a correct explanation for statement -1CStatement -1is true,Statement -2is FalseDStatement -1is False ,Statement -2is TrueSTATEMENT-1 Air bubble in glass medium behaves as concave lens.
STATEMENT2Lens formula is 1f=(μlensμmed−1)[1R1−1R2]ASTATEMENT -1is true statement 2 is true,Statement -2is a correct explanation for statement -1BSTATEMENT -1is true statement 2 is true,Statement -2is a not a correct explanation for statement -1CStatement -1is true,Statement -2is FalseDStatement -1is False ,Statement -2is True
Lens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
Let the given biconvex lens be divided in two equal parts, as shown in Fig. (a), along a section YY' which is perpendicular to the principal axis of lens. What is the power of each part?

View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
If two lens parts obtained in (b) are joined together as shown in Fig. (c), (i) what is the net power of the combination?
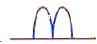
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
How is your answer modified if the given biconvex lens is divided into two parts along a section XX' along its principal axis ?
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
If twoplanoconvex lenses fromed as a result of (a) are joined together as shown in Fig. (b), what is the net power of the combination ?
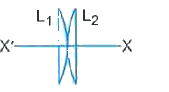
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
How is result of part (d) modified if two parts are placed together as shown in Fig. (c)(ii)?
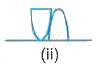
View Solution
