Find an expression for intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids. In which position of the polaroid sheet will the transmitted intensity be maximum?

Text Solution

Verified by Experts

Let us consider two .crossed polarisers $P_{1} and P_{2}$ with a polaroid sheet, $P_{3}$ placed between them.

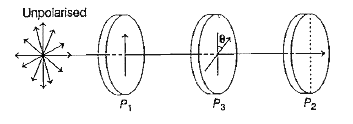
Let $I_{0}$ be the intensity of polarised light after passing through the first polariser $P_{1}$ . If $θ$ is the angle between the axes of $P_{1} and P_{3}$ , then the intensity of the polarised light after passing through $P_{3}$ will be $I = I_{0} {cos}^{2} θ$ . As, $P_{1} and P_{2}$ are crossed, the angle between the axes of $P_{1} and P_{2}$ is $90^{\circ}$ .
$∴$ Angle between the axes of $P_{2} and P_{3}$ is $(90^{\circ} - θ)$ .
The intensity of light emerging from $P_{2}$ will be given by
$I = [I_{0} {cos}^{2} θ] {cos}^{2} (90^{\circ} - θ)$
$I = [I_{0} {cos}^{2} θ] {sin}^{2} θ$
$\Rightarrow I = \frac{I_{0}}{4} (4 {cos}^{2} θ {sin}^{2} θ)$
$\Rightarrow I = \frac{I_{0}}{4} {(2 sin θ cos θ)}^{2}$
$\Rightarrow I = \frac{I_{0}}{4} {sin}^{2} (2 θ)$
The intensity of polarised light transmitted from $P_{2}$ will be maximum when
$sin 2 θ$ = maximum $= 1$
$\Rightarrow sin 2 θ = {sin 90}^{\circ} \Rightarrow 2 θ = θ = 45^{\circ}$
Also, the maximum transmitted intensity will be given by
$I = \frac{I_{0}}{4}$

Updated on:21/07/2023

|

Class 12 PHYSICS WAVE OPTICS AND INTERFERENCE

Similar Questions

Knowledge Check

When a polaroid sheet is rotated between two crossed polaroids, the intensity of the transmitted will be maximum, when angle $θ$ between pass axes is
A $\frac{π}{2}$
B $\frac{3 π}{4}$
C $\frac{π}{4}$
D $\frac{2 π}{3}$

Recommended Questions

Home
Ask Doubt
Profile