Question

State Bohr.s postulates for the theory of atomic model of hydrogen. Hence, deduce an expression for the total energy of the electron in the nth orbit.

Explanation

Expression for Total Energy A hydrogen atom consists of a tiny positively charged nucleus (with one proton) and an electron revolving in a stable circular orbit around the nucleus.

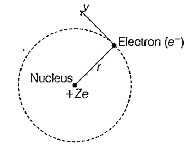
Let e, m and v be respectively, the charge, mass and velocity of the electron and `r_n` the radius of the orbit.
The positive charge on the nucleus is Ze, where Z is the atomic number in case of hydrogen atom, Z=1). As, the centripetal force is provided by the electrostatic force of attraction. We have,
`(mv_n^2)/(r_n) = (1)/(4pi epsi_0) . ((Ze) xx e)/(r_n^2) or mv_n^2 = (Ze^2)/(4pi epsi_0 r_n) ` ....(i)
From the second postulate, the angular momentum of the electron is
`mv_n r_n = n (h)/(2pi)` ....(ii)
where, n ( = 1, 2, 3, ....) is principal quantum number.
From Eqs. (i) and (ii), we get
Radius of nth orbit, `r_n = n^2 (h^2 epsi_0)/(pi m Ze^2) ` .....(iii)
The energy E of an electron in an orbit is the sum of kinetic and potential energies. Using Eq. (i), kinetic energy of electron is
`KE = 1/2 mv_n^2 = (Ze^2)/(8 pi epsi_0 r_n)` ....(iv)
The potential energy of the electron in an orbit of radius `r_n` due to the electrostatic attraction by the nucleus is given by
`PE = (1)/(4pi epsi_0 ) ((Ze)(-e))/(r_n)`
` = - (1)/(4pi epsi_0 ) . (Ze^2)/(r_n) ` ....(v)
The total energy of the electron is therefore
`E = KE+PE= (Ze^2)/(8pi epsi_0 r_n) - (Ze^2)/(4pi epsi_0 r_n) = - (Ze^2)/(8pi epsi_0 r_n)`
Substituting for `r_n` from Eq. (iii), we get
`E_n = - (mZ^2 e^4)/(8 epsi_0^2 h^2 ) ((1)/(n^2))`
where, n= 1, 2, 3, ... . This is the expression for the energy of the electron in the nth orbit.
For hydrogen atom Z = 1, substituting the standard values, we get `E_n = (-13.6)/(n^2) eV` , negative energy of the electron shows that the electron is bound to the nucleus and is not free to leave it. In ground state, n=1
`E_1 =-13.6 eV`