Deduce the relation , for refraction of light through prism .
The figure below shows the passage of light through a triangular prism ABC.
The angles of incidence and refraction at first face AB are I and .
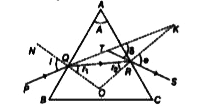
The angle between the emergent ray R and incident ray , PQ is called angle of deviation .
Here,
and
In the side QT has been produced outwards , Therefore , teh exterior angle should be equal to the sum of the interior opposite angles .
i.e
.....(i)
In .....(ii)
From quadrilateral AROQ , we have the sum of angles
This means that the sum of the remainin two angles should be
i.e ...(iii)
From Eqs. (ii) an (iii) we get
...(iv)
Substituting value from Eq. (iv) in Eq. (i) , we obtain
...(v)
When ,
[ prism in minimum deviation position ]
...(vi)
From Eq. (iv) ,
Putting in Eq. (v) , we get
This relation is called a prism formula .
Similar Questions
Knowledge Check
For the refraction of light through a prism
AFor every angle of deviation there are two angles of incidence.BThe light travelling inside an equilateral prism is necessarily parallel to the base when prism is set for minimum deviation.CThere are two angles of incidence for maximum deviation.DAngle of minimum deviation will increase if refractive index of prism is increased keeping the outside medium unchanged if μp>μsIn refraction of light through a prism the light ray:
Asuffers refraction only at one face of the prismBemergest out from the prism in a direction parallel to the incident rayCbends at both the surface of the prism towards its baseDbends at both the surfaces of the prism opposite to its base.
Refraction of light through Prism| condition of maximum and minimum deviation|Dispersion of light through Prism
View Solution(a) Draw the ray diagram showing refraction of ray of light through a glass prism. Derive the expression for the refractive index n of the material of prism in terms of the angle A ray angle of minimum deviation δm
(b) A ray of light PQ enters an isosceles right angles prism ABC of refractive index 1.5 as shown in figure .
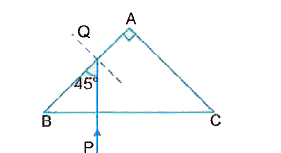
(i) Trace the path of the ray through the prism .
(ii) What will be the effect on the path of the ray if refractive index of the prism is 1.4 ?
View SolutionFor any prism, prove that .n. or μ=sin(A+δm2)sin(A2) where the terms have their usual meaning
View SolutionFor any prism, prove that .n. or μ=sin(A+δm2)sin(A2) where the terms have their usual meaning
View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
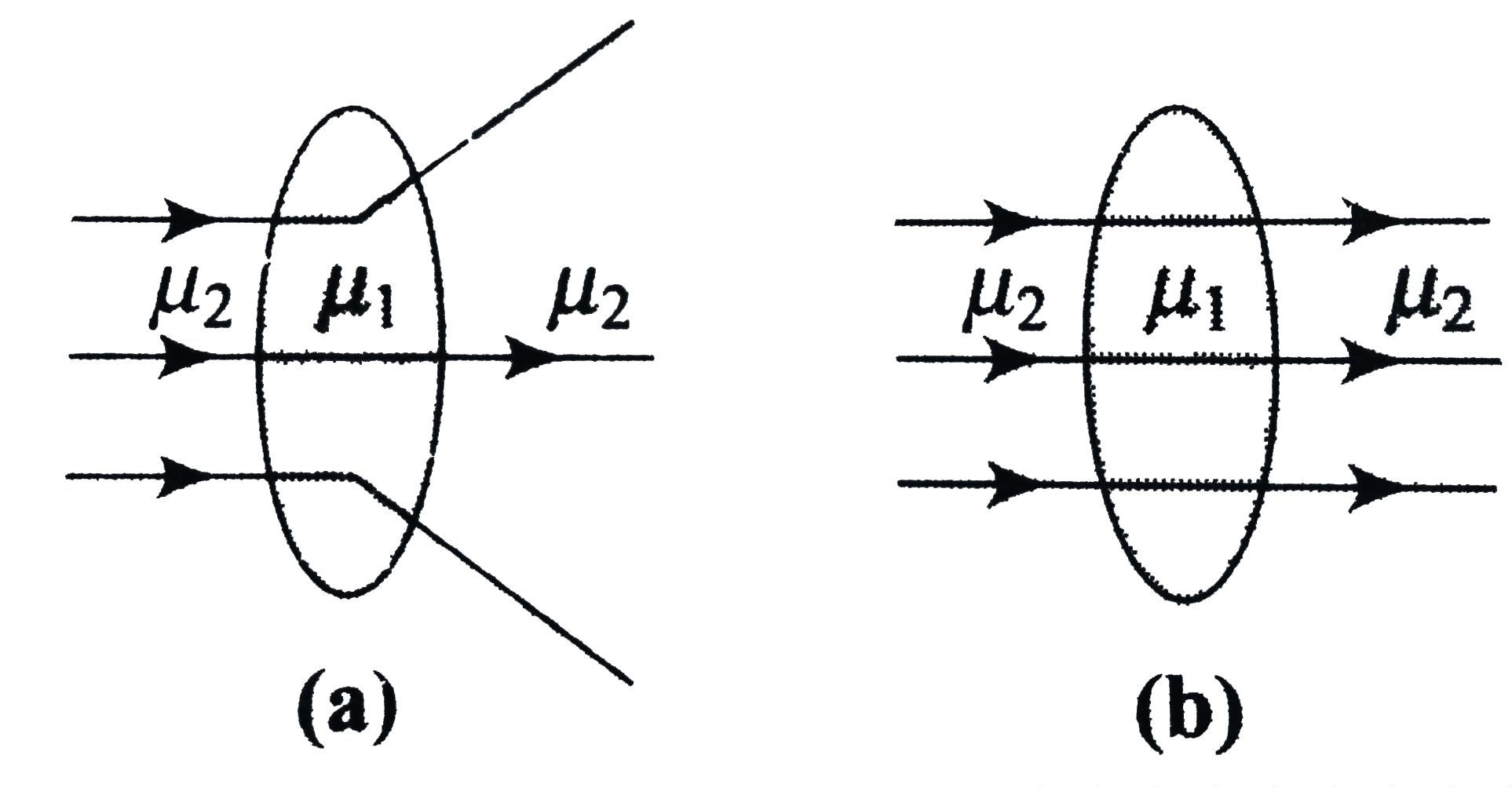
View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.

View Solution
