Question

Discuss Young.s double slit experiment. Derive its analytical expression for constructive and destructive interference.

Explanation

Young.s Double Slit Experiment In 1800-1801, Thomass Young was the first person to demonstrate experimently the interference of light. Here, a source of monochromatic light illuminates a rectangular narrow slit S, about 1mm wide, as shown in figure.

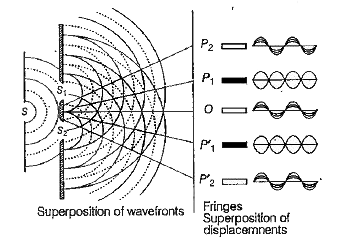
`S_(1) and S_(2)` are two parallel narrow slits which are arranged symmetrically and parallel to the slit S at a distance of about 10cm from it. The separation between `S_(1) and S_(2) " is " ~~2`mm and width of each slit is `~~3mm`. An observation screen is placed at a distance of `~~2m` from the two slits. Alternate bright and dark bands appear on the observation scrren. These are called interference fringes.
Theory of Interference of Waves
Let the waves from two coherent sources of light be represented as `y_(1) = a sin omega t and y_(2)= b sin (omega t+ phi)`
where, a and b are the respective amplitudes of the two waves and `phi` is the constant phase angle by which second wave leads the first wave. Applying superposition principle, the magnitude of the resultant displacement of the waves is
`y= y_(1) + y_(2)` or `y= a sin omega t + b sin (omega t+ phi) [because sin (A +B) = sin A cos B + cos A sin B]`
or `y= (a+ b cos phi) sin omega t + b sin phi cos omega t`
Putting `a+ b cos phi= A cos theta and b sin phi= A sin theta`
we get, `y= A cos theta.sin omega t+ A sin theta. cos omega t`
or `y= A sin (omega t+ theta)`

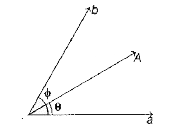
where, A is the resultant amplitude and `theta` is the resultant phase difference.
`therefore A= sqrt(a^(2) + b^(2) + 2ab cos phi) and tan theta= (b sin phi)/(a +b cos phi)`
As, intensity is directly proportional to the aquare of the amplitude of the wave, i.e., `I prop a^(2)`
So, for two different cases, `I_(1)= ka^(2), I_(2)= kb^(2)`
`therefore I_(R )= kA^(2)= k(a^(2) + b^(2) + 2ab cos phi)`
`therefore I_(R ) = I_(1) + I_(2) + 2 sqrt(I_(1)I_(2)) cos phi`
For Constructive Interference I should be maximum for which `cos phi=` maximum `=+1`
`therefore phi=0, 2pi, 4pi`.....
i.e. Phase difference `ph= 2n pi`
where, n= 1, 2,...
If `Delta x` be the path difference between the interfering waves, then
`Delta x= (lamda)/(2pi) phi= ((lamda)/(2pi))(2n pi)= n lamda`
`Delta x= n lamda and I_("max") prop (a+b)^(2)`
Hence, condition for constructive interference at a point is that, the phase difference between the two waves reaching the point should be zero or an even integral multiple of `2pi`. Equivalent path difference between the two waves reaching the point should be zero or an integral multiple of full wavelength.
For Destructive Interference
I should be minimum, for which `cos phi`= minimum = `-1`
`therefore phi= pi, 3pi, 5pi`
i.e., Phase difference, `phi= (2n-1) pi`
where n -1, 2, 3...
The corresponding path difference between the two waves is
`Delta x= ((lamda)/(2pi)) phi= ((lamda)/(2pi)) (2n-1) pi= (2n-1) (lamda)/(2)`
`therefore Delta x= (2n-1)= (lamda)/(2) and I_("min") prop (a-b)^(2)`
Hence, condition for destructive interference at a point is that, the phase difference between the two waves reaching the point should be an odd integral multiple of `pi` or path difference between the two waves reaching the point should be an odd integral multiple of half wavelength.