Prove the following identities:
tan2θ+cot2θ=sec2θcosec2θ−2Solution in Gujrati
Step by step video & image solution for Prove the following identities: tan^(2)theta+cot^(2)theta=sec^(2)thetacosec^(2)theta-2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INTRODUCTION TO TRIGONOMETRYBOOK - KUMAR PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - EXERCISE 8.1
18 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - KUMAR PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - EXERCISE 8.2
15 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - KUMAR PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Test Your Skills
41 Videos
- COORDINATE GEOMETRYBOOK - KUMAR PRAKASHANCHAPTER - COORDINATE GEOMETRYEXERCISE - Objective Questions (True or false)
5 Videos
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLES BOOK - KUMAR PRAKASHANCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Test Your Skills
48 Videos
Similar Questions
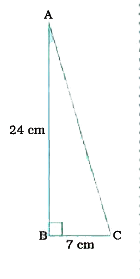
In ΔABC, right angled at B, AB=24cm,BC=7cm . Determine : sinA,cosA.
View SolutionEvaluate the following :
sin60∘cos30∘+sin30∘cos60∘
View SolutionIf tanθ=ab, find the value of cosθ+sinθcosθ−sinθ
View SolutionThe point (0,5), (0,-9) and (3,6) are collinear.
View SolutionIf the numerator of a fraction is decreased by 1. It reduces to 12 and if its numerator is increased by 1. it reduces to 1. Represent this situation algebraically and graphically.
View SolutionProve the following identities: tan2θ+cot2θ+2=sec2θcosec2θ
View SolutionProve the following identities: √sec2θ+cosec2θ=tanθ+cotθ
View SolutionProve the following identities: tanθ−cotθsinθcosθ=sec2θ−cosec2θ=tan2θ−cot2θ
View SolutionProve the following identity: (1+cotθ−cosecθ)(1+tanθ+secθ)=2
View SolutionProve the following identity: sec4θ−sec2θ=tan4θ+tan2θ
View SolutionProve each of the following identities :
tan2θ(1+tan2θ)+cot2θ(1+cot2θ)=1
View Solutionसिद्ध कीजिए:tan2θ+cot2θ=sec2θcosec2θ−2.
View Solutionसिद्ध कीजिए कि:
sec2θ+cosec2θ=sec2θcosec2θ.
View Solutionसिद्ध कीजिए tanθ1−cotθ+cotθ1−tanθ=1+tanθ+cotθ=1+secθcosecθ.
View Solutionत्रिकोणमितीय सर्वसमिकाओं को सिद्ध करो :
(1+cot2θ)tanθsec2θ=cotθ
View Solutionनिम्नलिखित सर्वसमिकाओं को सिद्ध करें :
tan4θ+tan2θ=sec4θ−sec2θ
View Solution
