Prove that opposite side of a quadrilateral circumscribing a circle subtend supple. Mentary angle at the center of the circle. 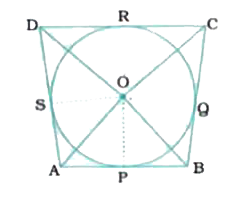
Text Solution
The correct Answer is:∠BOC+∠DOA=180∘
|
Topper's Solved these Questions
- CIRCLEBOOK - KUMAR PRAKASHANCHAPTER - CIRCLEEXERCISE - Objective Questions (Fill in the blanks)
5 Videos
- CIRCLEBOOK - KUMAR PRAKASHANCHAPTER - CIRCLEEXERCISE - Objective Questions
10 Videos
- CIRCLEBOOK - KUMAR PRAKASHANCHAPTER - CIRCLEEXERCISE - Exercise 10.1
7 Videos
- ARITHMETIC PROGRESSIONBOOK - KUMAR PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - OBJECTIVE QUESTIONS
1 Videos
- CONSTRUCTIONS BOOK - KUMAR PRAKASHANCHAPTER - CONSTRUCTIONS EXERCISE - OBJECTIVE QUESTIONS
25 Videos
Similar Questions
Knowledge Check
Find the perimeter of the quadrilateral that circumscribes this circle.
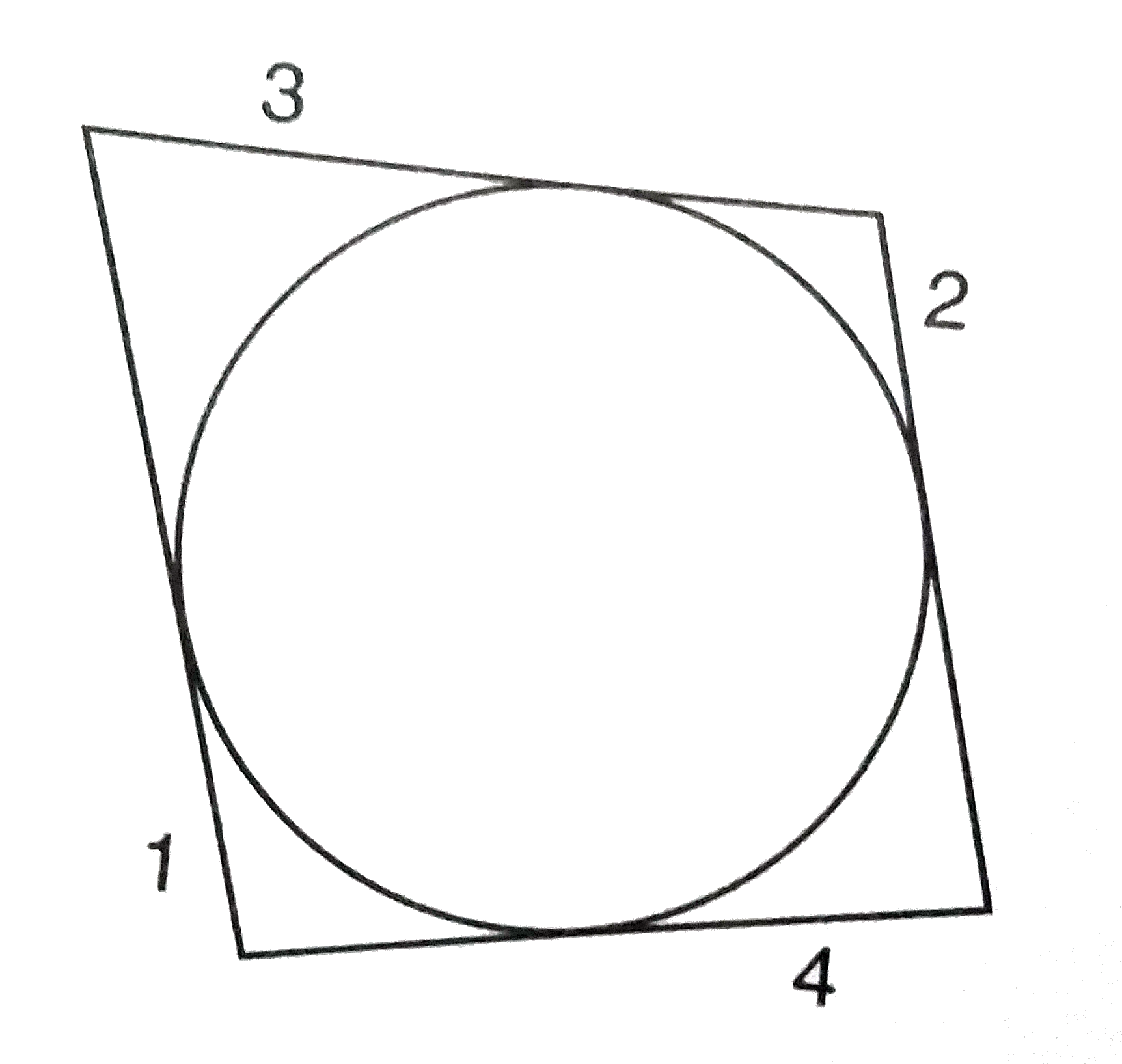 A10B12C15D20
A10B12C15D20
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle, subtend supplementary angles at the centre of a circle.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a Rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View Solution
