In a rectangle ABCD, E is the midpoint of AB, F is point on AC such that BF is perpendicular to AC and FE perpendicular to BD. Suppose BC=8√3. Find AB
The correct Answer is:24
Topper's Solved these Questions
- GEOMETRYBook:RESONANCEChapter:GEOMETRYExercise:Exercise-1 (Part-I: Previous Asked Question For Pre RMO)
Explore 50 Videos
- FUNDAMENTAL OF MATHEMATICSBook:RESONANCEChapter:FUNDAMENTAL OF MATHEMATICSExercise:Exercise
Explore 138 Videos
- INDEFINITE INTEGRATION Book:RESONANCEChapter:INDEFINITE INTEGRATION Exercise:SELF PRACTIC PROBLEMS
Explore 25 Videos
Similar Questions
AB is a straight line, C and D are points on the same side of AB such that AC is perpendicular to AB and DB is perpendicular to AB. Let AD and BC meet at E.
What is AEAD+DEBC equal to ?
View SolutionLet ABC be a triangle with AB=AC. If D is the midpoint of BC,E is the foot of the perpendicular drawn from D to AC,andF is the midpoint of DE, then prove that AF is perpendicular to BE.
View Solution
Knowledge Check
In ΔABC,AB=AC,Ois a point on BC such that BO = CO and OD is perpendicular to AB and OE is perpendicular to AC. If ∠BOD=30∘ then measure of ∠AOE is
A45∘B60∘C75∘D30∘In ΔABC,D is the midpoint of AC, F is a point AB such that CF bisects BD at E. If AF = 18 cm, then the length of BF is :
A12 cmB8 cmC6 cmD9 cmLet ABC be a triangle such that AB=BC. Let F be midpoint of AB and X be a poin on BC such that FX is perpendicular to AB. If BX =3XC then the ratio BC/AC equals
A√3B√2C√32D1
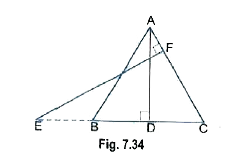
In the given Fig. 7 .34, AB = AC. E is a point on CB produced. If AD is perpendicular to BC and EF perpendicular to AC, prove that ΔABD is similar to ΔCEF.
View SolutionLet AB be a line segment with midpoint C, and D be the midpoint of AC. Let C1 be the circle with diameter AB and C2 be the circle with diameter AC. Let E be a point on C1 such that EC is perpendicular to AB. Let f be a point on C2such that DF is perpendicular to AB. Then, the value of sin∠FEC is
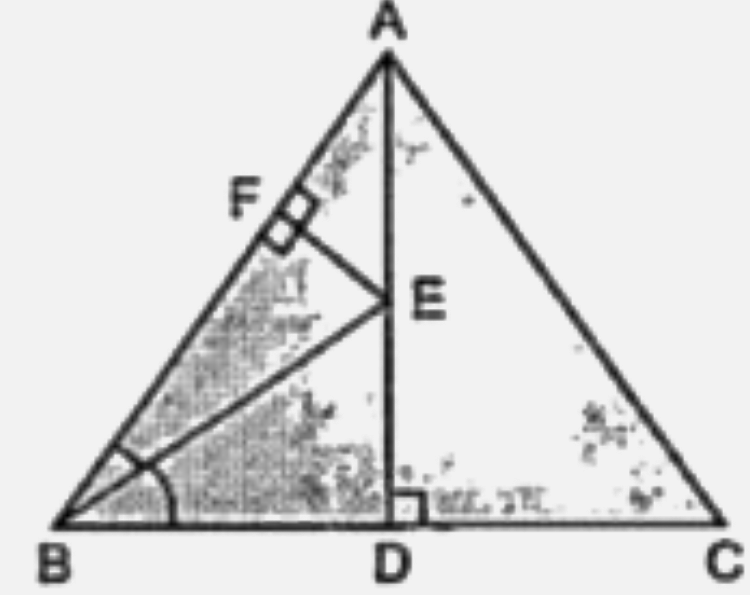
View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED=EF
View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that :
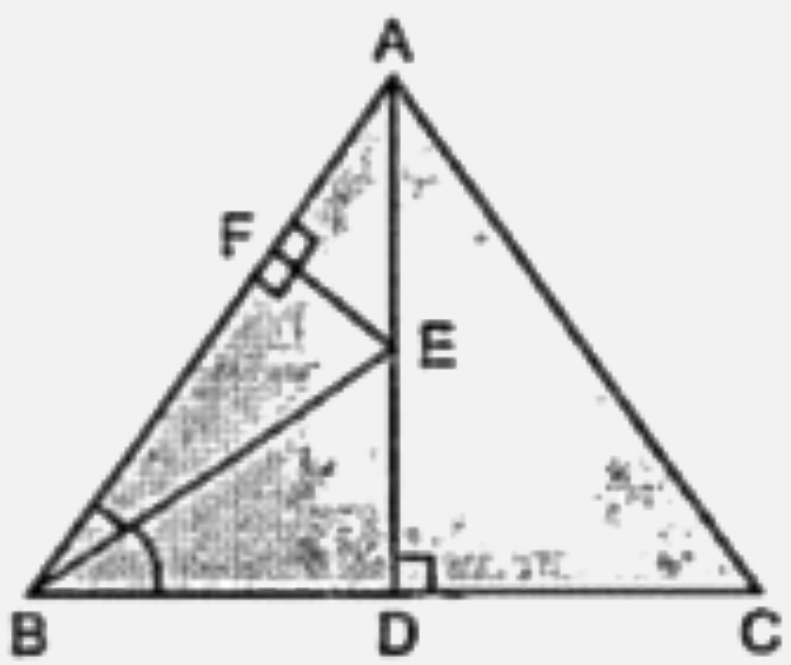
ED=EF
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD is perpendicular to EF.
View Solution
