In a triangle ABC, the median from B to CA is perpendicular to the median from C to AB. If the median from A to BC is 30, determine (BC2+CA2+AB2)/100
Text Solution
The correct Answer is:24
|
Topper's Solved these Questions
- GEOMETRYBOOK - RESONANCECHAPTER - GEOMETRYEXERCISE - Exercise-1 (Part-I: Previous Asked Question For Pre RMO)
50 Videos
- FUNDAMENTAL OF MATHEMATICSBOOK - RESONANCECHAPTER - FUNDAMENTAL OF MATHEMATICSEXERCISE - Exercise
138 Videos
- INDEFINITE INTEGRATION BOOK - RESONANCECHAPTER - INDEFINITE INTEGRATION EXERCISE - SELF PRACTIC PROBLEMS
25 Videos
Similar Questions
Knowledge Check
Let 'l' is the length of median from the vertex A to the side BC of a ΔABC. Then
A4l2=2b2+2c2−a2B4l2=b2+c2+2bccosAC4l2=a2+4bccosAD4l2=(2s−a)2sin2A2If in a triangle ABC, BE and CF are two medians perpendicular to each other and if AB=19 cm and AC=22cm then the length of BC is
A19.5 cmB26 cmC20.5 cmD13 cmLet 'l' is the length of median from the vertex A to the side BC of a ΔABC. Then
A4l2=2b2+2c2−a2B4l2=b2+c2+2bccosAC4l2=a2+4bccosAD4l2=(2s−a)2sin2A2
In △ABC , AB=10
AC=7,BC=9
then find the length find the length of the median drawn from point C to side AB .
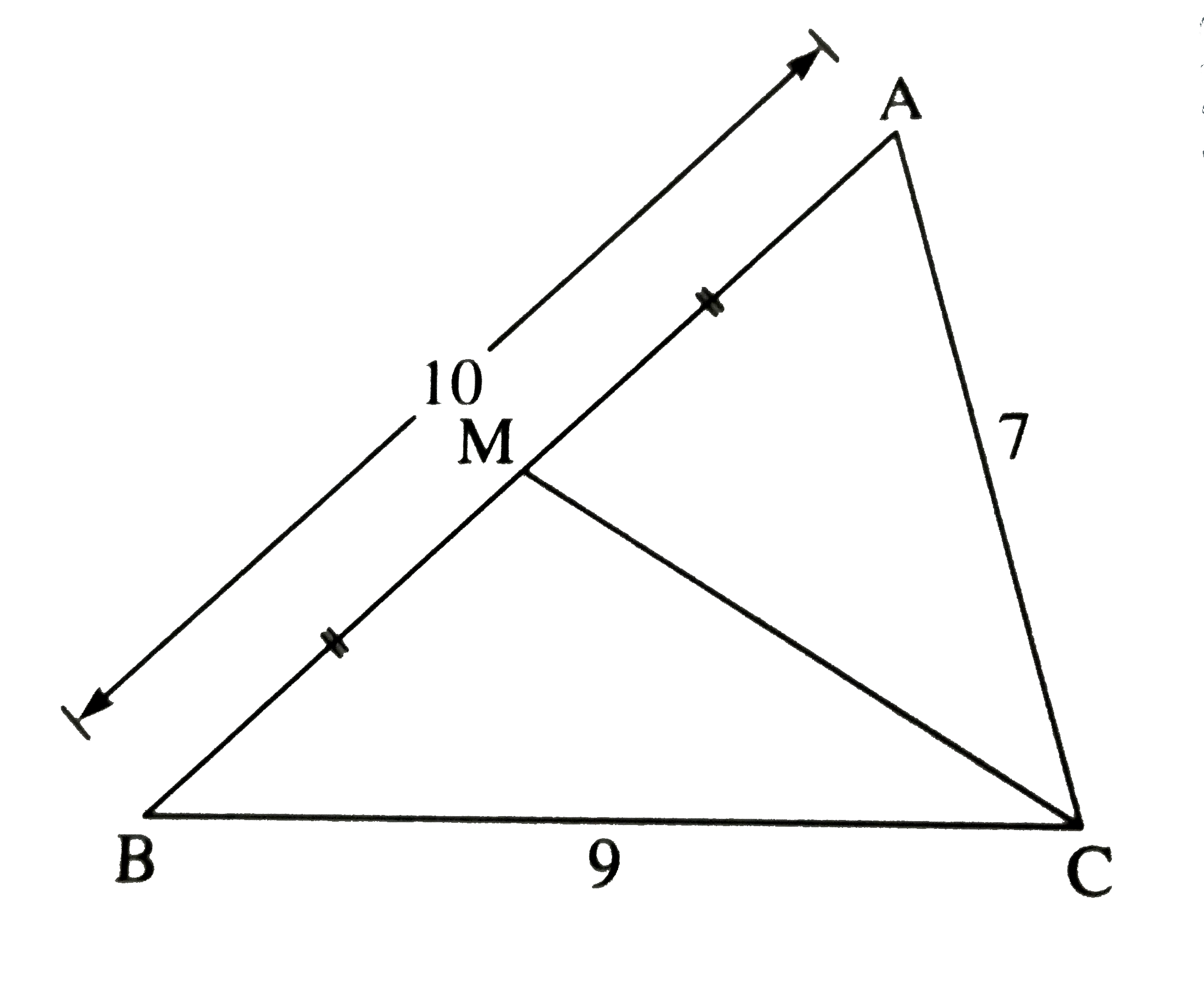
View SolutionLet 'l' is the length of median from the vertex A to the side BC of a ΔABC. Then
View SolutionIf AD, BE and CF are the medians of a ΔABC, then evaluate (AD2+BE2+CF2):(BC2+CA2+AB2).
View SolutionIf AD, BE and CF are the medians of a ΔABC, then evaluate (AD2+BE2+CF2):(BC2+CA2+AB2).
View SolutionIn an equilateral triangle ABC, BE is perpendicular to side CA. Prove that:
AB2+BC2+CA2=4BE2
View Solution
