AB সরলরেখার বহিঃস্থ বিন্দু O থেকে AB সরলরেখার ওপর OC সরলরেখাংশ লম্ব। OD এবংOE এমন দুটি তির্যক সরলরেখাংশ যে , CD>CE ।প্রমাণ করো OD>OE ।
Step by step video & image solution for AB সরলরেখার বহিঃস্থ বিন্দু O থেকে AB সরলরেখার ওপর OC সরলরেখাংশ লম্ব। OD এবংOE এমন দুটি তির্যক সরলরেখাংশ যে , CD gt CE ।প্রমাণ করো OD gt OE । by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
30 জন লোক 15 দিনে একটি গ্রামের রাস্তার 37 অংশ সারান যদি আরো 10 জন লোক কাজটি করতে আসেন তাহলে রাস্তাটির বাকি অংশ সারাতে কতদিন লাগবে ত্রৈরাশিক পদ্ধতিতে হিসাব করো।
View SolutionIn the figure, OD is the bisector of ∠AOC, OE is the bisector of ∠BOC and OD ⊥ OE. Show that the points A, O and B are collinear.
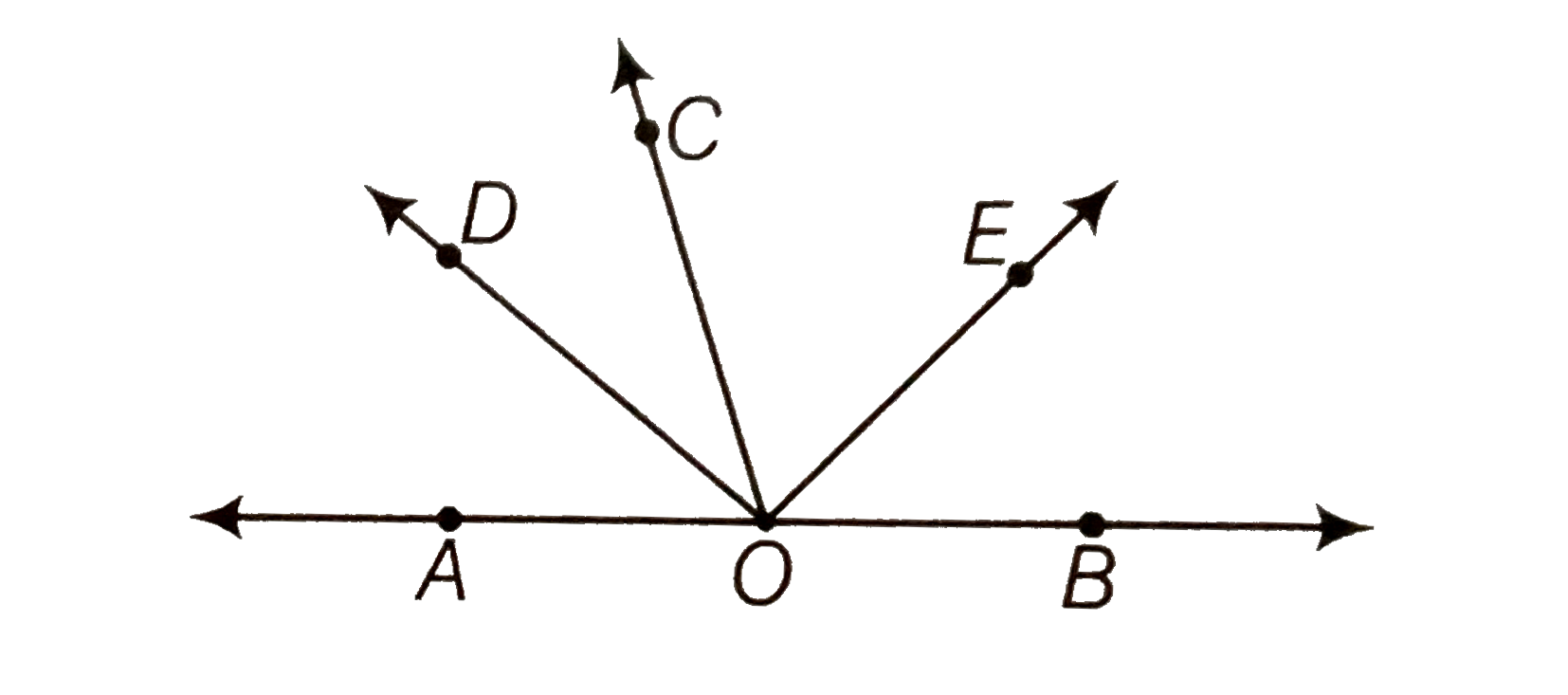
View Solutionसरल रेखा AB में O एक बिंदु है । OC तथा OD विपरीत दिशाओं में पर AB खींचे गये लम्ब हैं। सिद्ध करें कि OC तथा OD एक ही सरल रेखा में है।
View Solutionif D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABCandO be any points, then prove that OA+OB+OC=OD+OE+OF
View Solutionसमलंब ABCD में AB।।CD इसके विकर्ण परस्पर O पर प्रतिच्छेद करते है तो सिद्ध कीजिए कि AOOC=BOOD.
View SolutionΔABC के अंदर बिंदु O से भुजाओ BC,CA और AB पर क्रमश: लंब OD,OE और OF डाले गए है। सिद्ध कीजिए कि
AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2.
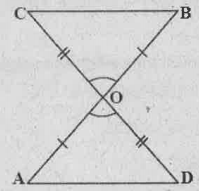
View Solutionఇచ్చిన పటంలో AB మరియు CD లు 'O' వద్ద ఖండించుకొనుచున్నాయి. OA=OB మరియు OD=OC అయిన AD∣∣BC అని నిరూపించండి.
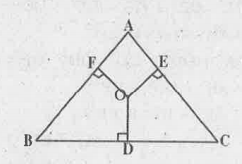
View Solutionత్రిభుజము ABC అంతరంలో ఏదైనా బిందువు 'O' OD⊥BC,OE⊥AC మరియు OF⊥AB అయిన OA2+OB2+OC2−OD2−OE2−OE2=AE2+BD2+CE2
View Solutionমনে করো xy সমতলে অবস্থিত S একটি বৃত্ত, যা x2+y2 = 4 সমীকরণ দ্বারা সংজ্ঞাত। মনে করো S বৃত্তের ওপর P এমন একটি বিন্দু যার স্থানাঙ্ক দুটি (x স্থানাঙ্ক ও yস্থানাঙ্ক) ধনাত্মক। মনে করো P বিন্দুতে S বৃত্তের স্পর্শক অক্ষদ্বয়কে M ও N বিন্দুতে ছেদ করেছে। তবে MN সরলরেখার মধ্যবিন্দু যে বক্রের ওপর অবস্থিত, তা হল—
View SolutionIn the figure, OD is the bisector of ∠AOC, OE is the bisector of ∠BOC and OD ⊥ OE. Show that the points A, O and B are collinear.

View SolutionIn the given figure, O is a point in the interior of a DeltaABC, OD⊥BC,OE⊥AC and OF⊥AB. Show that :
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2.
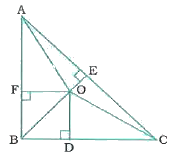
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2 .
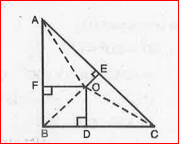
View SolutionIn a Δ≤ABC the bisectors of ∠Band∠C meet AC and AB at D and E respectively . BD and CE intersect at O. If Od = OE then
View Solutionਚਿੱਤਰ 6.54 ਵਿੱਚ, ΔABC ਦੇ ਵਿਚ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ O ਹੈ ਅਤੇ OD⊥BC,OE⊥AC ਅਤੇ OF⊥ABਹੈ।ਦਿਖਾਓ ਕਿ OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
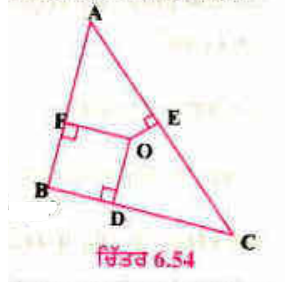
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABC and O be any point, then prove that OA+OB+OC=OD+OE+OF
View Solutionसरल रेखा AB में O एक बिंदु है। OC तथा OD विपरीत दिशाओं में खींचिए गए लम्ब है सिद्ध करें कि OC तथा OD एक ही सरल रेखा में है |

View Solution
