In the figure, OD is the bisector of ∠AOC, OE is the bisector of ∠BOC and OD ⊥ OE. Show that the points A, O and B are collinear. 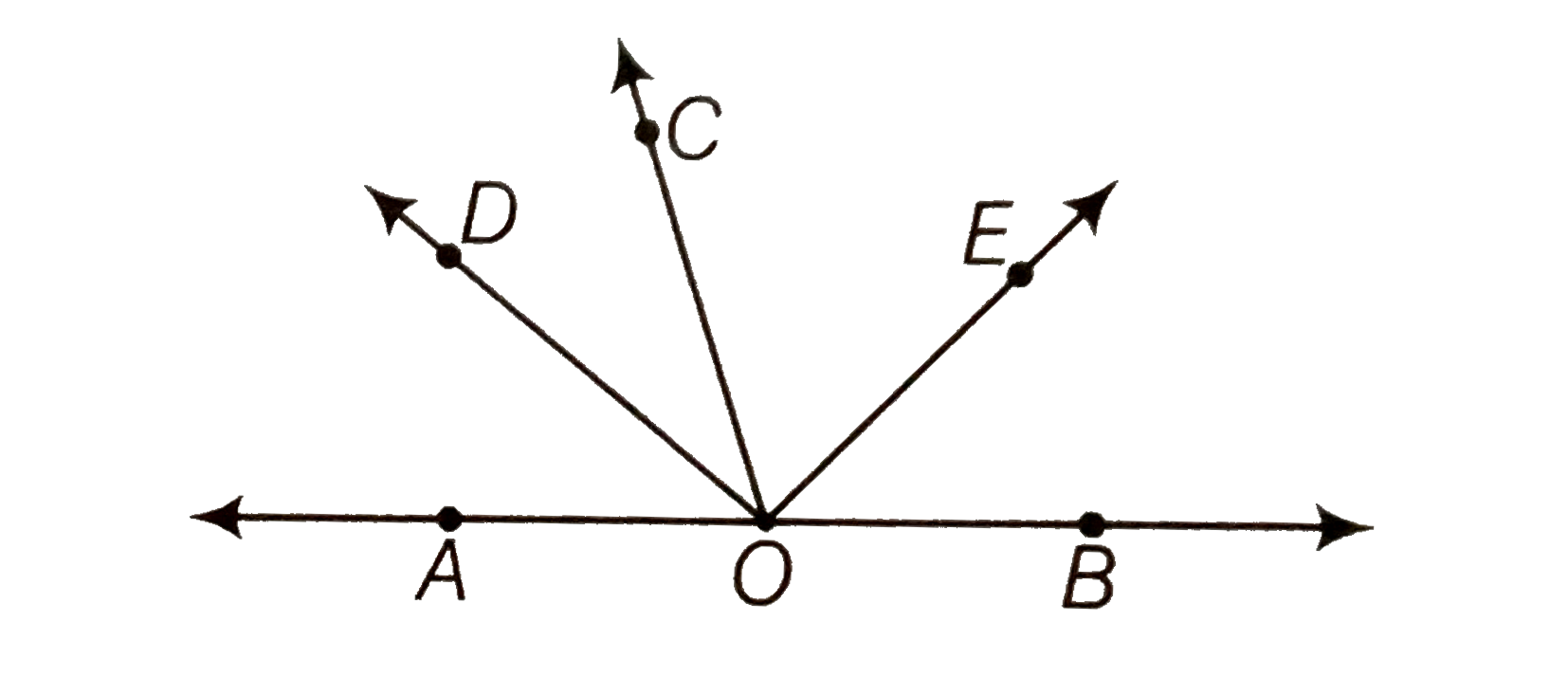
Given In the figure, OD ⊥OE,OD and OE and bisectors of ∠AOC and ∠BOC.
To show Points A, O and B are collinear i.e., AOB is a straight line.
Proof Since, OD and OD and OE bisect angles ∠AOC and ∠BOC, repectively.
∴ ∠AOC=2∠DOC
and ∠COB=2∠COE
On adding Equ. (i) and (ii), we get
and ∠COB=2∠COE
⇒ ∠AOC+∠COB=2∠(DOC+∠COE)
⇒ ∠AOC+∠COB=2∠DOC
⇒ ∠AOC+∠COB=2×90∘
⇒ ∠AOC+∠COB=180∘
∴ ∠AOB=180∘
So, ∠AOCand∠COB are forming linear pair.
Also, AOB is a straight line.
Hence, point A, O and B are collinear.
Topper's Solved these Questions
Similar Questions
In the figure, O is the center of the circle and BO is the bisector of ∠ABC show that AB=BC
View SolutionIn Figure, AC>AB and AD is the bisector of ∠A . Show that ADC>∠ADB .
View SolutionIn the given figure, O is the centre of the circle. If chord AB= chord AC, OP⊥ABandOQ⊥AC, show that: PB= QC

View SolutionIn Figure, if AD is the bisector of LA , show that: AB>BD (ii) AC>CD
View SolutionIn the given figure, AD is altitude and AE is bisector of angle BAC of ΔABC. Show that ΔDAE=12(∠B−∠C)

View SolutionIn figure, AB and CD are straight lines and OP and OQ are respectively the bisectors of angles ∠BOD and ∠AOC . Show that the rays OP and OQ are in the same line.
View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View SolutionIn triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View SolutionIn the Figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionThe bisectors of angles A and B of a scalene triangle ABC meet at O.
What is the point O called ?
View Solution
