ABCD সামান্তরিকের ক্ষেত্রফল 100 বর্গএকক, BC বাহুর মধ্যবিন্দু P, ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত?
Step by step video & image solution for ABCD সামান্তরিকের ক্ষেত্রফল 100 বর্গএকক, BC বাহুর মধ্যবিন্দু P, ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
x, y, z তিনটি বাস্তব সংখ্যা। x<y,y<z⇒—
View Solution1 সংখ্যাটি –
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP Calculate:
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP Calculate
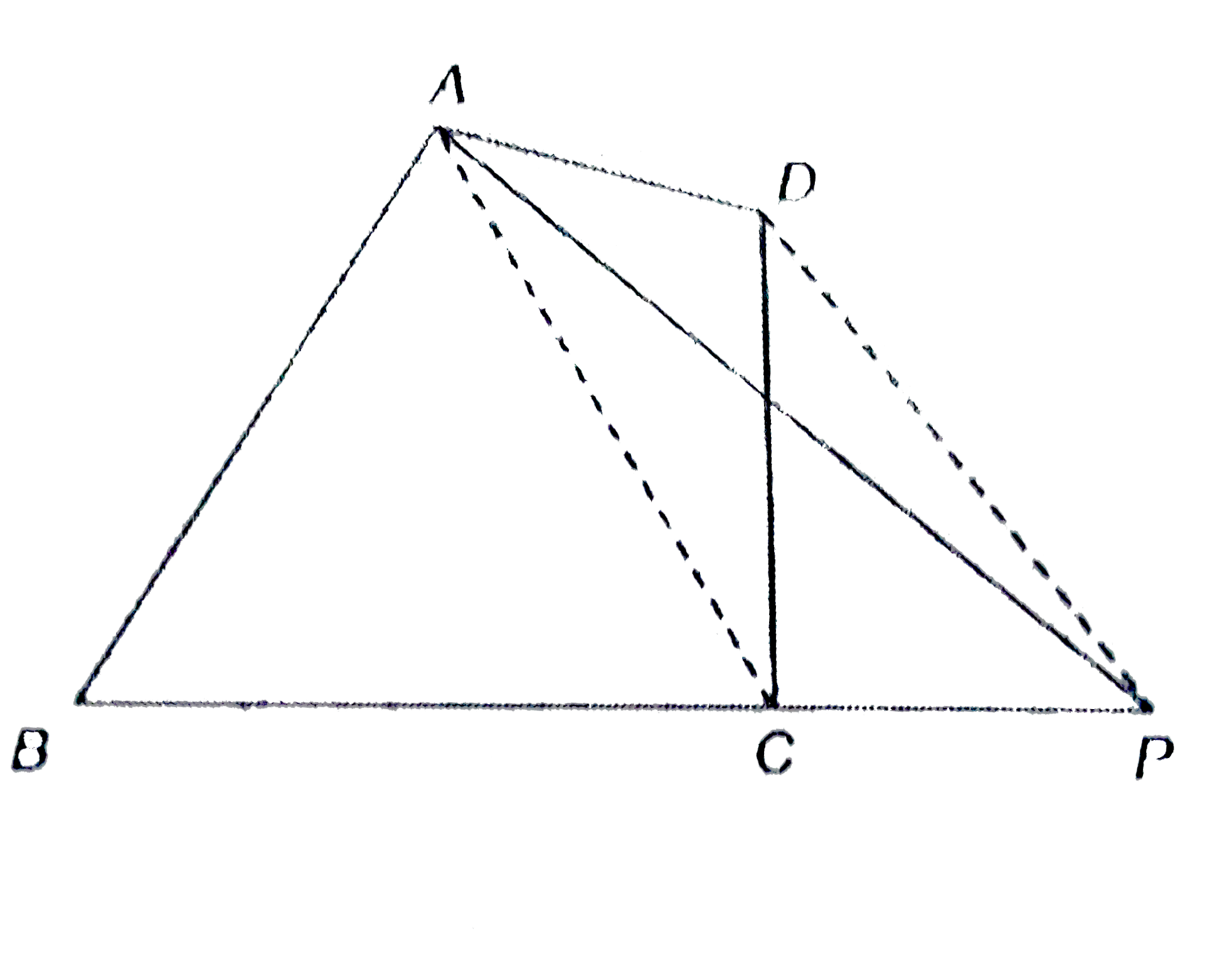
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
area of ΔABP= area of □ABCD
View Solution
In rectangle ABCD, point P divide BC such that BP is 25% of the length of BC. If the area of quadrlateral ABPD is 34, what is the area of rectangle ABCD?
View SolutionThe area of the parallelogram ABCD is 100 sq. units. P is the mid-point of BC. Determine the area of the ΔABP.
View SolutionABCD समलंब है DC∣∣AB और P,BC का मध्य - बिन्दु है। सिध्द कीजिए।
(समलंब ABCD )=2 ar1 (ΔAPD)
View Solutionযে ত্রিভুজের শীর্ষ বিন্দু তিনটি o,z এবং z(cosalpha+isinalpha)(0ltalphaltpi) জটিল রাশির দ্বারা সূচিত হয় তার ক্ষেত্রফল হবে-
View SolutionIn the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:

ΔABP≅ΔDCQ
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
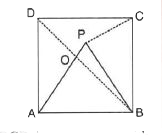
∠AOB
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
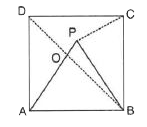
∠BPC
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
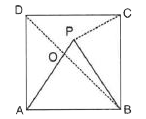
∠PCD
View SolutionIn a parallelogram ABCD, P is a point on side AD such that 3AP = AD and Q is a point on BC such that 3CQ = BC. Prove that : AQCP is a parallelogram.
View SolutionTriangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
ΔABP≅ΔACP
View SolutionABCD is a parallelogram and P is a point of ¯¯¯¯¯¯CD. Show that ar(△ABP) = ar(△ADP+△BCP).
View Solution
