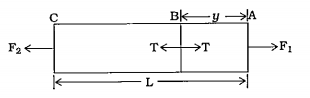
આકૃતિમાં દર્શાવ્યા પ્રમાણે L લંબાઈના સળિયાના બે છેડા પર અસમાન બળો F1અને F2 (F2<F1) લાગે છે, તો A છેડાથી y અંતરે સળિયામાં ઉદૂભવતો તણાવ શોધો..
T=F1(yL)+F2(1−(yL))
T=F1(1+(yL))−F2(yL)
T=F1(1−(yL))+F2(yL)
T=F1(yL)−F2(1+(yL))
The correct Answer is:C
Step by step video & image solution for આકૃતિમાં દર્શાવ્યા પ્રમાણે L લંબાઈના સળિયાના બે છેડા પર અસમાન બળો F_1અને F_2 (F_2 < F_1) લાગે છે, તો A છેડાથી y અંતરે સળિયામાં ઉદૂભવતો તણાવ શોધો.. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
એક કણ બળ F=7−2x+3x2 ની અસર હેઠળ X-અક્ષ પર x=0 થી x=5m સુધી ગતિ કરે છે. આ પ્રક્રિયામાં થતું કાર્ય કેટલું ?
03:02View Solutionભૂસ્થિર ઉપગ્રહની ભ્રમણકક્ષાની ત્રિજ્યા કરતાં ચોથા ભાગની ત્રિજ્યા ધરાવતી વર્તુળાકાર કક્ષામાં પરિભ્રમણ કરતા ઉપગ્રહનો આવર્તકાળ શોધો.
04:37View Solutionद्रवचालित लिफ्ट में उत्थापक बल F2 तथा आरोपित बल F1 अनुपात F2/F1 कहलाता है
01:55View SolutionFind the magnitude of F_1 and F_2 . If F_1, F_2 make angle 30^@ and 45^@ with F_3 and magnitude of F_3 is 10 N. ("given "vecF_1 + F_2 = vecF_3)
01:05View Solutionबहुलक ज्ञात करने के सूत्र l+(f1−f02f1−f0−f2)x में f1 को........ कहते हैं।
02:25View Solutionयदि l=10, f0=5,f1=10 तथाf2=5 h=2 बहुलक होगा -
06:48View SolutionThe function f1 and f2 are defined as follows : f1=a!+b!andf2=aa+bb for a, b > 1 and a, b in N then the correct relation is :
04:32View SolutionShow that if f1andf2 are one-one maps from R→R, then the product f1×f2:R→R defined by (f1×f2)(x)=f1(x)f2(x) need not be one-one.
04:20View SolutionSuppose f1andf2 are non-zero one-one functions from R→R. is f1f2 necessarily one-one? Justify your answer. Here, f1f2:R→R is given by (f1f2)(x)=f1(x)f2(x) for all x∊Rdot
04:27View SolutionSuppose f1andf2 are non=zero one-one functions from R→R. is f1f2 necessarily one-one? Justify your answer. Here, f1f2:R→R is given by (f1f2)(x)=f1(x)f2(x) for all xR.
02:54View SolutionGive examples of two one-one functions f1 and f2 from R to R such that f1+f2:R→R , defined by (f1+f2)(x)=f1(x)+f2(x) is not one-one.
06:00View SolutionGive examples of two surjective function f1 and f2 from Z to Z such that f1+f2 is not surjective.
01:05View SolutionSuppose f1 and f2 are non-zero one-one functions from R to R . Is f1f2 necessarily one-one? Justify your answer. Here, f1f2:R→R is given by (f1f2)(x)=f1(x)f2(x) for all x∈R .
02:48View SolutionThe formula of mode is....a)L+[f1−f02f1−f0−f2]×h b)L−[f1−f02f1−f0−f2]×h c)L+[f1−f02f1−f0+f2]×h d)L+[f1−f02f2−f0−f2]×h
05:46View SolutionIf P=(x , y),F_1=(3,0),F_2=(-3,0), and 16 x^2+25 y^2=400 , then P F_1+P F_2 equal
03:20View Solution

