Four identical solid spheres each of mass and radius are fixed at four corners of a light square frame of side length such that centres of spheres coincides with corners of square, moment of inertia of spheres about an axis passing through any side of square is
The correct Answer is:D
To solve the problem of finding the moment of inertia of four identical solid spheres, each of mass M and radius R, fixed at the corners of a square frame of side length 4R, we will follow these steps:
Step 1: Understand the Configuration
We have four identical solid spheres located at the corners of a square with side length 4R. The centers of the spheres coincide with the corners of the square.
Step 2: Identify the Axis of Rotation
We need to calculate the moment of inertia about an axis that passes through one side of the square. Let's denote the corners of the square as A, B, C, and D.
Step 3: Calculate the Moment of Inertia for Spheres A and B
The spheres at corners A and B lie on the axis of rotation. The moment of inertia I for a solid sphere about its own axis is given by:
I=25MR2
Since both spheres A and B are on the axis, their contributions to the moment of inertia are:
IA=IB=25MR2
Thus, the total moment of inertia for spheres A and B is:
IAB=IA+IB=2×25MR2=45MR2
Step 4: Calculate the Moment of Inertia for Spheres C and D
Spheres C and D are not on the axis of rotation. We will use the parallel axis theorem to find their contributions. The distance from the axis to the centers of spheres C and D is 2R (half the side length of the square).
Using the parallel axis theorem:
I=Icm+Md2
where Icm=25MR2 (moment of inertia about their own center) and d=2R.
Thus, for spheres C and D:
IC=25MR2+M(2R)2=25MR2+4MR2=25MR2+205MR2=225MR2
The same calculation applies to sphere D:
ID=225MR2
Step 5: Total Moment of Inertia
Now we can find the total moment of inertia I by summing the contributions from all four spheres:
I=IAB+IC+ID
Substituting the values we found:
I=45MR2+225MR2+225MR2
Calculating this gives:
I=45MR2+445MR2=485MR2
Final Answer
Thus, the moment of inertia of the four spheres about an axis passing through any side of the square is:
485MR2
We have four identical solid spheres located at the corners of a square with side length 4R. The centers of the spheres coincide with the corners of the square.
We need to calculate the moment of inertia about an axis that passes through one side of the square. Let's denote the corners of the square as A, B, C, and D.
The spheres at corners A and B lie on the axis of rotation. The moment of inertia I for a solid sphere about its own axis is given by:
Spheres C and D are not on the axis of rotation. We will use the parallel axis theorem to find their contributions. The distance from the axis to the centers of spheres C and D is 2R (half the side length of the square).
Now we can find the total moment of inertia I by summing the contributions from all four spheres:
Thus, the moment of inertia of the four spheres about an axis passing through any side of the square is:
Similar Questions
Four particle of mass m each are placed at four corners of a square ABCD of side a. Point O is the centre of the square. Moment of inertia of all four particles about an axis passing through
View SolutionFour spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then moment of inertia of the system about an axis about one of the sides of the square is :-
View SolutionThe moment of inertia of a system of four rods, each of length l and mass m, about the axis shown is:

View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View SolutionFour identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertia about
View SolutionFour solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of I0 & IA , where I0 is the moment of inertia of the system about an axis through the centre of the square and IA is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)
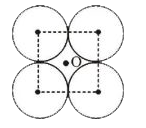
View SolutionFour solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of I0 & IA , where I0 is the moment of inertia of the system about an axis through the centre of the square and IA is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)

View SolutionFour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionFour identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
View Solution
