Four identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
a2√2
a3√2
a4√2
a5√2
The correct Answer is:D
To solve the problem of finding the shift in the center of mass when one of the four identical particles at the corners of a square has its mass doubled, we can follow these steps:
1. Initial Configuration:
- We have four identical particles, each of mass m, placed at the corners of a square with side length a.
- The coordinates of the particles are:
- P1(0,0)
- P2(a,0)
- P3(0,a)
- P4(a,a)
2. Calculate Initial Center of Mass (CM):
- The formula for the center of mass for a system of particles is given by:
RCM=∑miri∑mi
- For the initial configuration:
RCM=m(0,0)+m(a,0)+m(0,a)+m(a,a)4m
- This simplifies to:
RCM=(0+a+0+a,0+0+a+a)4=(2a,2a)4=(a2,a2)
3. New Configuration After Doubling One Mass:
- Let’s say we double the mass of the particle at P1. Now the masses are:
- P1(0,0) with mass 2m
- P2(a,0) with mass m
- P3(0,a) with mass m
- P4(a,a) with mass m
4. Calculate New Center of Mass:
- The new center of mass is calculated as:
R′CM=2m(0,0)+m(a,0)+m(0,a)+m(a,a)2m+m+m+m=(0+a+0+a,0+0+a+a)5m
- This simplifies to:
R′CM=(2a,2a)5=(2a5,2a5)
5. Calculate the Shift in Center of Mass:
- The initial center of mass was at (a2,a2) and the new center of mass is at (2a5,2a5).
- The shift d in the center of mass is given by:
d=√(2a5−a2)2+(2a5−a2)2
- Simplifying the x-coordinates:
2a5−a2=4a−5a10=−a10
- Therefore:
d=√2(−a10)2=√2⋅a2100=√2a2100=a√210
6. Final Result:
- The shift in the center of mass is:
d=a√210
- We have four identical particles, each of mass m, placed at the corners of a square with side length a.
- The coordinates of the particles are:
- P1(0,0)
- P2(a,0)
- P3(0,a)
- P4(a,a)
- The formula for the center of mass for a system of particles is given by:
RCM=∑miri∑mi
- For the initial configuration:
RCM=m(0,0)+m(a,0)+m(0,a)+m(a,a)4m
- This simplifies to:
RCM=(0+a+0+a,0+0+a+a)4=(2a,2a)4=(a2,a2)
- Let’s say we double the mass of the particle at P1. Now the masses are:
- P1(0,0) with mass 2m
- P2(a,0) with mass m
- P3(0,a) with mass m
- P4(a,a) with mass m
- The new center of mass is calculated as:
R′CM=2m(0,0)+m(a,0)+m(0,a)+m(a,a)2m+m+m+m=(0+a+0+a,0+0+a+a)5m
- This simplifies to:
R′CM=(2a,2a)5=(2a5,2a5)
- The initial center of mass was at (a2,a2) and the new center of mass is at (2a5,2a5).
- The shift d in the center of mass is given by:
d=√(2a5−a2)2+(2a5−a2)2
- Simplifying the x-coordinates:
2a5−a2=4a−5a10=−a10
- Therefore:
d=√2(−a10)2=√2⋅a2100=√2a2100=a√210
- The shift in the center of mass is:
d=a√210
Similar Questions
Four identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View Solution
Knowledge Check
- Question 1 - Select One
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−√2Gm2l(2−1√2)B−2Gm2l(2+1√2)C−√2Gm2l(√2−1√2)D−2Gm2l(√2−1√2)
Four particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionThree identical spheres each of radius .R. are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is
View SolutionSeven particles are placed at the seven corners of a cube of side 'a' (except at origin ) . The mass of each particle is 'm' . The centre of mass of the system is
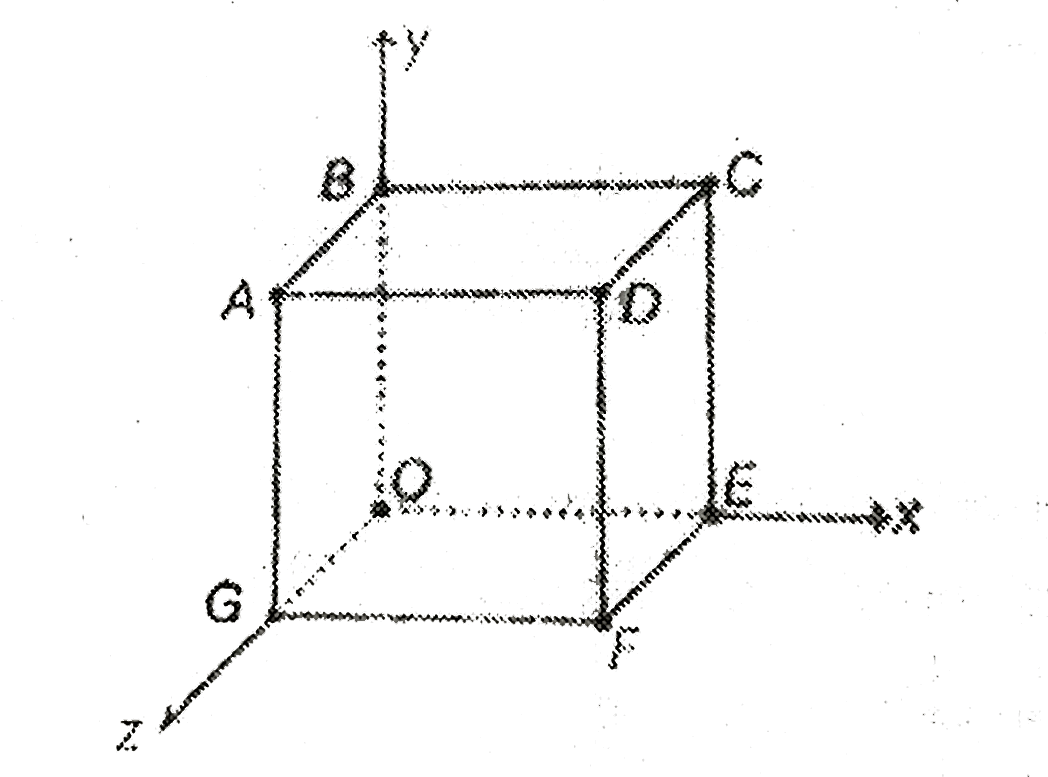 View Solution
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.
 View Solution
View SolutionFour identical particles of mass M are located at the corners of a square of side 'a'. What should be their speed if each of them revolves under the influence of others' gravitational field in a circular orbit circumscribing the square?
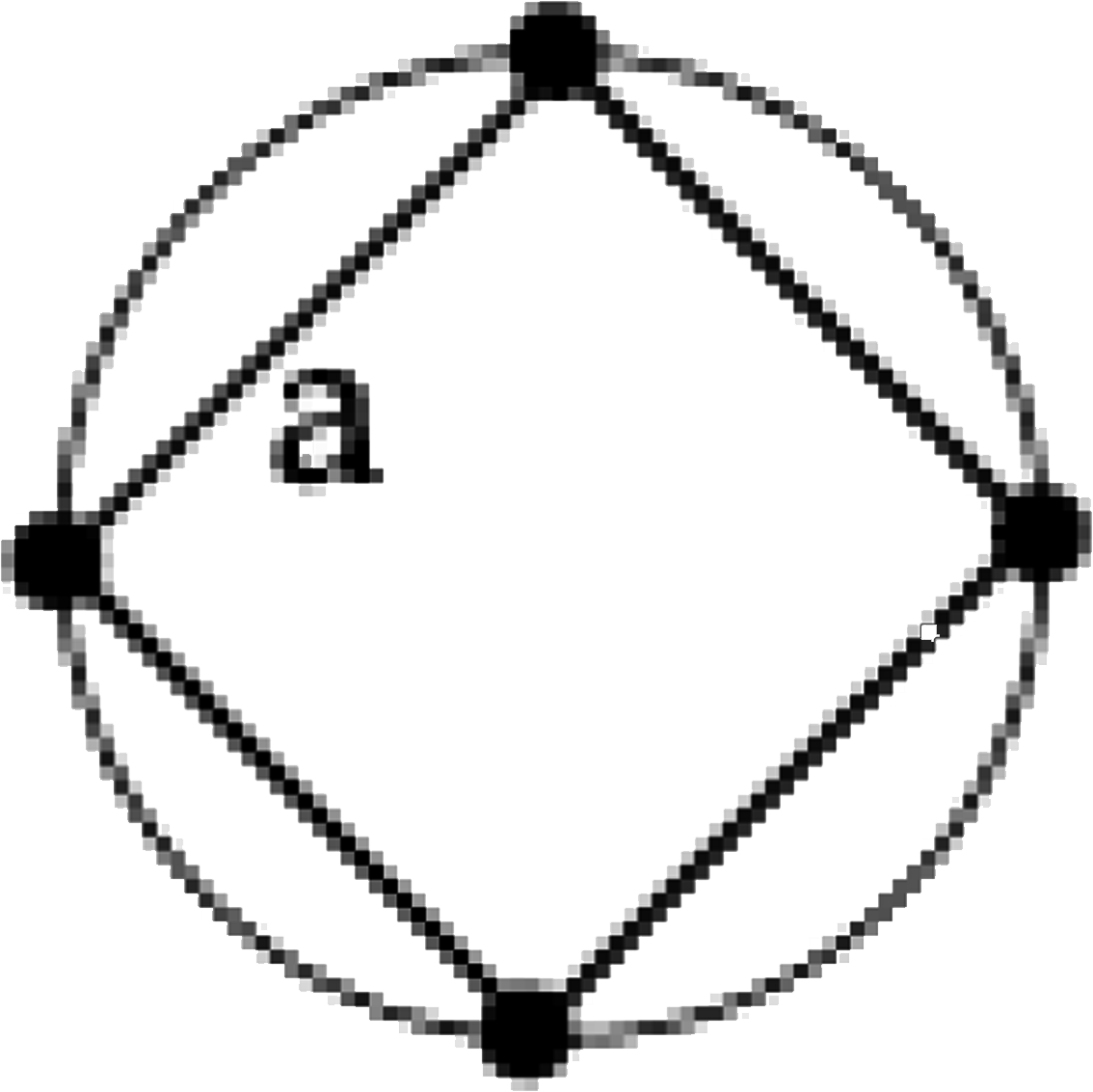 View Solution
View SolutionFour particles of masses 2,2,4,4 kg are arranged at the corners A,B,C,D of a square ABCD of side 2m as shown in the figure. The perpendicular distance of their centre of mass from the side AB is
 View Solution
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View Solution

