A coil having N turns is would tightly in the form of a spiral with inner and outer radii a and b respectively. When a current I passes through the coil, the magnetic field at the centre is.
μ0NIb
μ0NIa
μ0NI2(b−a)ln(ba)
μ0NI(b−a)ln(ba)
The correct Answer is:C
To find the magnetic field at the center of a coil wound in the form of a spiral with inner radius a and outer radius b, we can follow these steps:
1. Understanding the Coil Structure:
- The coil has N turns and is tightly wound in a spiral shape with inner radius a and outer radius b.
2. Consider an Element of the Coil:
- We can consider a thin ring element of thickness dr at a distance r from the center. The number of turns in this thin ring can be expressed as dn.
3. Finding the Number of Turns in the Element:
- The total number of turns N is distributed over the radial distance from a to b. Therefore, the number of turns per unit length can be given by:
Nb−a
- Thus, the number of turns dn in the thickness dr is:
dn=Nb−a⋅dr
4. Magnetic Field Contribution from the Element:
- The magnetic field dB at the center due to this thin ring is given by:
dB=μ0⋅I⋅dn2πr
- Substituting dn:
dB=μ0⋅I2πr⋅Nb−a⋅dr
5. Integrating to Find Total Magnetic Field:
- To find the total magnetic field B at the center, we integrate dB from r=a to r=b:
B=∫badB=∫baμ0⋅I⋅N2π(b−a)⋅drr
- This integral simplifies to:
B=μ0⋅I⋅N2π(b−a)⋅(ln(r))ba
- Evaluating the integral gives:
B=μ0⋅I⋅N2π(b−a)⋅(ln(b)−ln(a))=μ0⋅I⋅N2π(b−a)⋅ln(ba)
6. Final Expression for the Magnetic Field:
- Thus, the magnetic field at the center of the coil is:
B=μ0⋅N⋅I2π(b−a)⋅ln(ba)
- The coil has N turns and is tightly wound in a spiral shape with inner radius a and outer radius b.
- We can consider a thin ring element of thickness dr at a distance r from the center. The number of turns in this thin ring can be expressed as dn.
- The total number of turns N is distributed over the radial distance from a to b. Therefore, the number of turns per unit length can be given by:
Nb−a
- Thus, the number of turns dn in the thickness dr is:
dn=Nb−a⋅dr
- The magnetic field dB at the center due to this thin ring is given by:
dB=μ0⋅I⋅dn2πr
- Substituting dn:
dB=μ0⋅I2πr⋅Nb−a⋅dr
- To find the total magnetic field B at the center, we integrate dB from r=a to r=b:
B=∫badB=∫baμ0⋅I⋅N2π(b−a)⋅drr
- This integral simplifies to:
B=μ0⋅I⋅N2π(b−a)⋅(ln(r))ba
- Evaluating the integral gives:
B=μ0⋅I⋅N2π(b−a)⋅(ln(b)−ln(a))=μ0⋅I⋅N2π(b−a)⋅ln(ba)
- Thus, the magnetic field at the center of the coil is:
B=μ0⋅N⋅I2π(b−a)⋅ln(ba)
Similar Questions
A long insulated copper wire is closely wound as a spiral of N turns. The spiral has inner radius a and outer radius b. The spiral lies in the xy-plane and a steady current I flows through the wire. Thez-component of the magetic field at the centre of the spiral is

View SolutionOne of the two identical conducting wires of length L is bent in the form of a circular loop and the other one into a circular coil of N identical turns. If the same current passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the central of the coil (BC), i.e. BLBC will be :
View SolutionConsider a co axial cable which consists of an inner wilre of radius a surrounded by an outer shell of inner and outer radii b and c respectively. The inner wire caries a current I and outer shell carries an equal and opposite current. The magnetic field at a distance x from the axis where b<x<c is
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
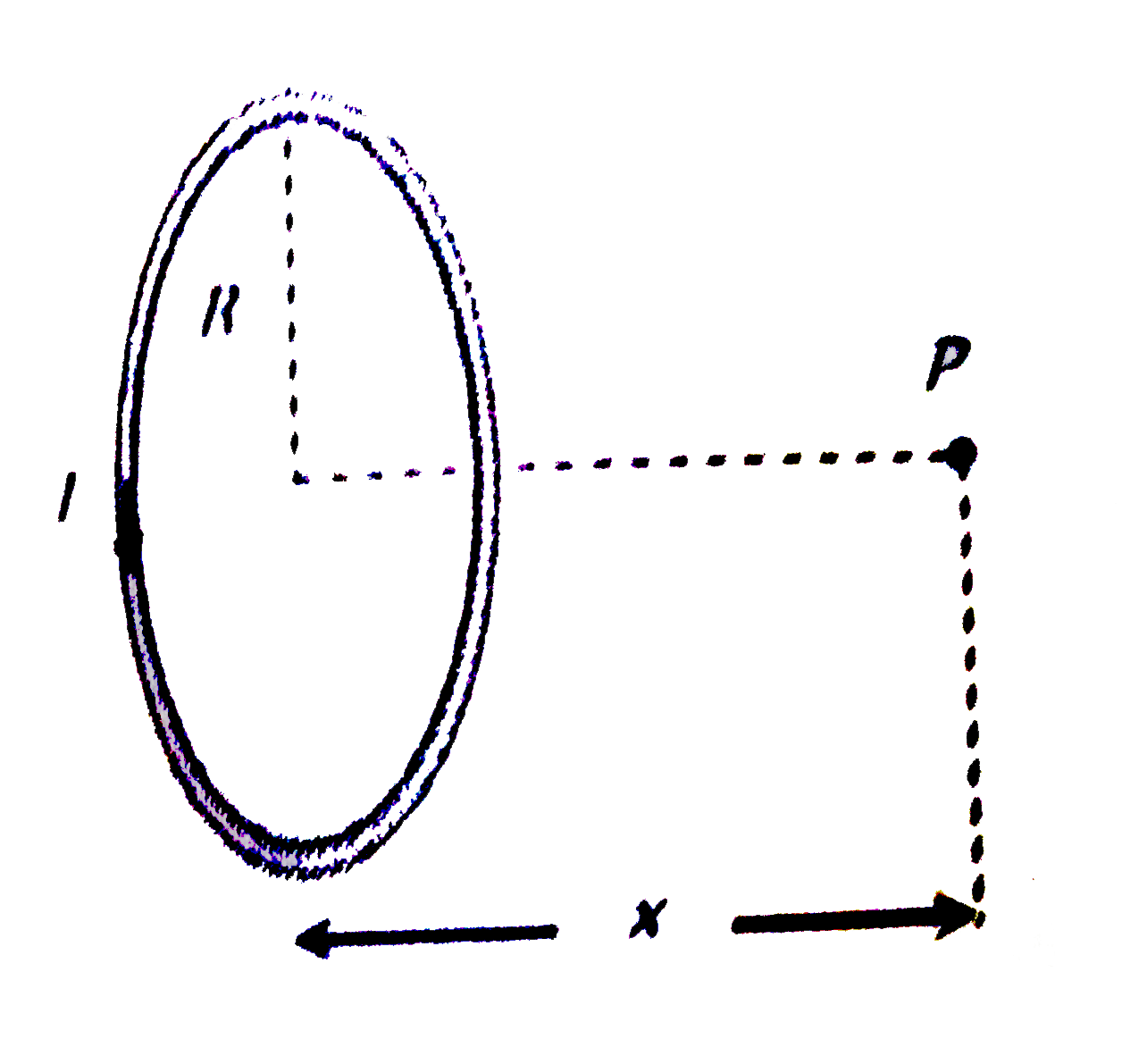
View SolutionA circular coil of radius 1⋅5cmcarriesacurrentof1⋅5A. If the coil has 25 turns , find the magnetic field at the centre.
View SolutionA circular coil carrying a certain, current produces a magnetic field B0 at its center. The coil is now rewound so as to have 3 turns and the same currents is passed through it. The new magnetic field at the center is
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 2I is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionWhen current is passed through a circular wire prepared from a conducting material, the magnetic field produced at its centre is B. Now a loop having two turns is prepared from the same wire and the same current is passed through it. The magnetic field at its centre will be :
View SolutionA thin insulated wire form a spiral of N=100 turns carrying a current of i=8mA . The inner and outer radii are equal to a=5cm and b=10cm. Find the magnetic field at the centre of the coil.

View Solution
