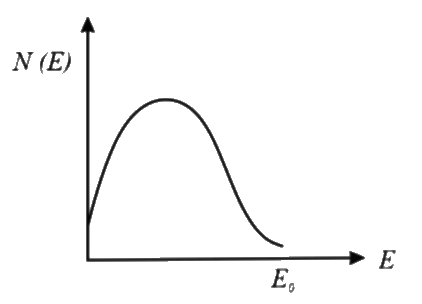
The energy spectrum of β - particle [number N(E) as a function of β - energy E] emitted from a radioactive source is
The correct Answer is:A
To solve the problem regarding the energy spectrum of beta particles emitted from a radioactive source, we need to analyze the behavior of the number of emitted beta particles (N(E)) as a function of their energy (E). The question provides us with four options in the form of graphs, and we need to determine which graph correctly represents this relationship.
1. Understanding Beta Particle Emission:
- Beta particles are emitted during radioactive decay and have a continuous energy spectrum ranging from 0 to a maximum energy (E_max). The number of beta particles emitted at a specific energy level (N(E)) varies with energy.
2. Analyzing the Energy Spectrum:
- At very low energies (E ≈ 0), the number of emitted beta particles (N(E)) is expected to be at its maximum because there are many particles with low energy.
- As the energy increases towards the maximum energy (E_max), the number of emitted beta particles decreases. This is due to the nature of the decay process and the distribution of energy among the emitted particles.
3. Identifying the Correct Graph:
- We need to find a graph that starts at a high value of N(E) when E is 0 and decreases as E approaches E_max.
- The correct graph should reflect this behavior: high N(E) at low E, tapering off to low N(E) as E approaches E_max.
4. Evaluating the Options:
- Option 1: Starts high at E = 0 and decreases as E increases. This matches our expectations.
- Option 2: Shows an increase in N(E) as E increases, which is incorrect.
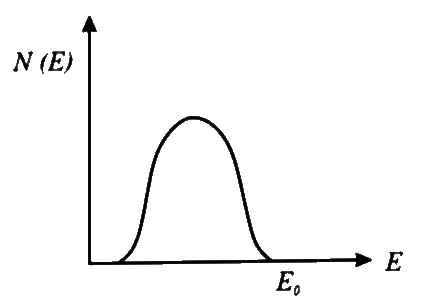
- Option 3: Shows a constant value and then a decrease, which does not fit the expected behavior.
- Option 4: Similar to option 3, starts high but does not show the correct decrease pattern.
5. Conclusion:
- Based on the analysis, Option 1 is the correct representation of the energy spectrum of beta particles emitted from a radioactive source.
Final Answer:
The correct option is Option 1.
- Beta particles are emitted during radioactive decay and have a continuous energy spectrum ranging from 0 to a maximum energy (E_max). The number of beta particles emitted at a specific energy level (N(E)) varies with energy.
- At very low energies (E ≈ 0), the number of emitted beta particles (N(E)) is expected to be at its maximum because there are many particles with low energy.
- As the energy increases towards the maximum energy (E_max), the number of emitted beta particles decreases. This is due to the nature of the decay process and the distribution of energy among the emitted particles.
- We need to find a graph that starts at a high value of N(E) when E is 0 and decreases as E approaches E_max.
- The correct graph should reflect this behavior: high N(E) at low E, tapering off to low N(E) as E approaches E_max.
- Option 1: Starts high at E = 0 and decreases as E increases. This matches our expectations.
- Option 2: Shows an increase in N(E) as E increases, which is incorrect.
- Option 3: Shows a constant value and then a decrease, which does not fit the expected behavior.
- Option 4: Similar to option 3, starts high but does not show the correct decrease pattern.
- Based on the analysis, Option 1 is the correct representation of the energy spectrum of beta particles emitted from a radioactive source.
The correct option is Option 1.
Similar Questions
Knowledge Check
The electron emitted in beta radiation originates from
Ainner orbits of atomBfree electron existing in nucleiCdecay of a neutron in a nucleusDphoton escaping from the nucleus
In the disintegration of a radioactive element, α- and β-particles are evolved from the nucleus.
.0n1→.1H1+.−1e0+ Antineutrino + Energy
4.1H1→.2He4+2.+1e0+ Energy
Then, emission of these particles changes the nuclear configuration and results into a daughter nuclide. Emission of an α-particles results into a daughter element having atomic number lowered by 2 and mass number by 4, on the other hand, emission of a β-particle yields an element having atomic number raised by 1.
How many α- and β-particle should be emitted from a radioactive nuclide so that an isobar is formed?
View SolutionThe total energy of a particle in SHM is E. Its kinetic energy at half the amplitude from mean position will be
View SolutionWhat are the respective number of α and β-particles emitted in the following radioactive decay?
View SolutionDuring alpha-decay , a nucleus decays by emitting an α-particle ( a helium nucleus .2He4) according to the equation
.AZX→.A−4Z−2Y+.42He+Q
In this process, the energy released Q is shared by the emitted α-particle and daughter nucleus in the form of kinetic energy .
The energy Q is divided in a definite ratio among the α-particle and the daughter nucleus .
A nucleus that decays spontaneously by emitting an electron or a positron is said to undergo β-decay .This process also involves a release of definite energy . Initially, the β-decay was represented as .AZX→.AZ+1Y+e−(electron)+Q
According to this reaction, the energy released during each decay must be divided in definite ratio by the emitted e' (β-particle) and the daughter nucleus. While , in alpha decay, it has been found that every emitted α-particle has the same sharply defined kinetic energy. It is not so in case of β-decay . The energy of emitted electrons or positrons is found to vary between zero to a certain maximum value. Wolfgang Pauli first suggested the existence of neutrinoes in 1930. He suggested that during β-decay, a third particle is also emitted. It shares energy with the emitted β particles and thus accounts for the energy distribution.
The beta particles (positron) are emitted with different kinetic energies because
View SolutionDuring alpha-decay , a nucleus decays by emitting an α-particle ( a helium nucleus .2He4) according to the equation
.AZX→.A−4Z−2Y+.42He+Q
In this process, the energy released Q is shared by the emitted α-particle and daughter nucleus in the form of kinetic energy .
The energy Q is divided in a definite ratio among the α-particle and the daughter nucleus .
A nucleus that decays spontaneously by emitting an electron or a positron is said to undergo β-decay .This process also involves a release of definite energy . Initially, the β-decay was represented as .AZX→.AZ+1Y+e−(electron)+Q
According to this reaction, the energy released during each decay must be divided in definite ratio by the emitted e' (β-particle) and the daughter nucleus. While , in alpha decay, it has been found that every emitted α-particle has the same sharply defined kinetic energy. It is not so in case of β-decay . The energy of emitted electrons or positrons is found to vary between zero to a certain maximum value. Wolfgang Pauli first suggested the existence of neutrinoes in 1930. He suggested that during β-decay, a third particle is also emitted. It shares energy with the emitted β particles and thus accounts for the energy distribution.
During β+ decay (positron emission) a proton in the nucleus is converted into a neutron, positron and neutrino. The reaction is correctly represented as
View SolutionFrom a radioactive substance x numbers of α-particles any y numbers of β-particles are emitted. As a result atomic number decreases by n and mass number by m. Then, match the following two columns.
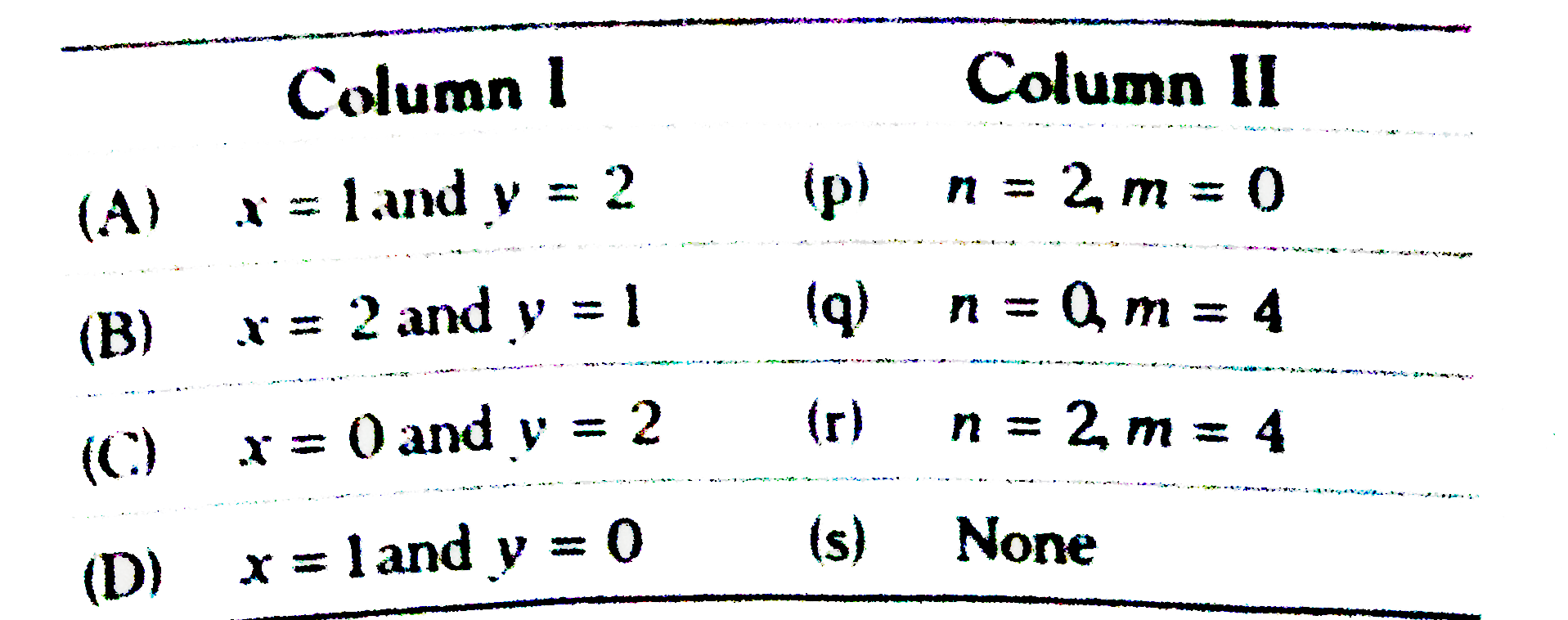
View SolutionIn the disintegration of a radioactive element, α- and β-particles are evolved from the nucleus.
.0n1→.1H1+.−1e0+ Antineutrino + Energy
4.1H1→.2He4+2.+1e0+ Energy
Then, emission of these particles changes the nuclear configuration and results into a daughter nuclide. Emission of an α-particles results into a daughter element having atomic number lowered by 2 and mass number by 4, on the other hand, emission of a β-particle yields an element having atomic number raised by 1.
A radioactive element belongs to IIIB group, it emits ona α- and β-particle to form a daughter nuclide. The position of daughter nuclide will be in
View Solution
