A marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
0.02
0.03
0.06
0.01
The correct Answer is:C
To find the coefficient of friction for the marble block, we can follow these steps:
Step 1: Identify the known values
- Mass of the marble block, m=2kg
- Initial velocity, u=6m/s
- Final velocity, v=0m/s (since the block stops)
- Time taken to stop, t=10s
Step 2: Use the first equation of motion
We can use the first equation of motion to find the acceleration (or deceleration in this case):
v=u+at
Substituting the known values:
0=6+a⋅10
Rearranging to solve for a:
a⋅10=−6⟹a=−610=−0.6m/s2
The negative sign indicates that this is a deceleration (retardation).
Step 3: Apply the force balance equation
The frictional force acting on the block can be expressed as:
Ffriction=μmg
where μ is the coefficient of friction and g is the acceleration due to gravity (approximately 9.8m/s2).
According to Newton's second law, the net force acting on the block is also equal to:
Fnet=ma
Since the only horizontal force acting on the block is the frictional force, we can set these equal:
μmg=ma
Step 4: Solve for the coefficient of friction μ
We can cancel m from both sides (as long as m≠0):
μg=a
Now, substituting the values we have:
μ⋅9.8=−0.6
Solving for μ:
μ=−0.69.8≈−0.0612
Since the coefficient of friction cannot be negative, we take the absolute value:
μ≈0.0612
Conclusion
The coefficient of friction μ is approximately 0.06.
- Mass of the marble block, m=2kg
- Initial velocity, u=6m/s
- Final velocity, v=0m/s (since the block stops)
- Time taken to stop, t=10s
We can use the first equation of motion to find the acceleration (or deceleration in this case):
v=u+at
Substituting the known values:
0=6+a⋅10
Rearranging to solve for a:
a⋅10=−6⟹a=−610=−0.6m/s2
The negative sign indicates that this is a deceleration (retardation).
The frictional force acting on the block can be expressed as:
Ffriction=μmg
where μ is the coefficient of friction and g is the acceleration due to gravity (approximately 9.8m/s2).
Fnet=ma
Since the only horizontal force acting on the block is the frictional force, we can set these equal:
μmg=ma
We can cancel m from both sides (as long as m≠0):
μg=a
Now, substituting the values we have:
μ⋅9.8=−0.6
Solving for μ:
μ=−0.69.8≈−0.0612
Since the coefficient of friction cannot be negative, we take the absolute value:
μ≈0.0612
The coefficient of friction μ is approximately 0.06.
Similar Questions
A block of mass 2kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 5s. The coefficient of friction between the block and ice is (g=10 ms−2)
View SolutionA block slides on ice with a velocity of 5m/s comes to rest after moving through a distance of 13.5m . Find the coefficient of friction ?
View Solution
Knowledge Check
A block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 N
A man of mass 60 kg sitting on ice pushes a block of mass of 12kg on ice horizontally with a speed of 5 ms−1. The coefficient of friction between the man and ice and between block and ice is 0.2. If g =10 ms−2, the distances between man and the block, when they come to rest is
View SolutionA large slab of mass 5kg lies on a smooth horizontal surface, with a block of mass 4kg lying on the top of it. The coefficient of friction between the block and the slab is 0.25. If the block is pulled horizontally by a force of F =6N, the work done by the force of friction on the slab, between the instants t=2s and t=3s, is (g=10ms−2)

View SolutionA body of mass 10 kg moves on rough horizontal surface with initial velocity 10m/s and travels 500m before coming to rest. The coefficient of friction is
View SolutionA block of mass 5 kg slides down a rough inclined surface. The angle of inclination is 45∘. The coefficient of sliding friction is 0.20. When the block slides 10 cm, the work done on the block by force of friction is
View SolutionA block of mass m is given an initial downward velocity v0 and left on inclined place ( coefficient of friction =0.6). The block will
View SolutionIn the given diagram, the block of mass 2 kg and 3 kg are placed one over the other . The contact surfaces are rough with coefficient of friction μ1=0.2,μ92)=0.06) . A force F=12t N ( where t is in second ) is applied on upper block in the direction ( Given that g = 10m/s2)
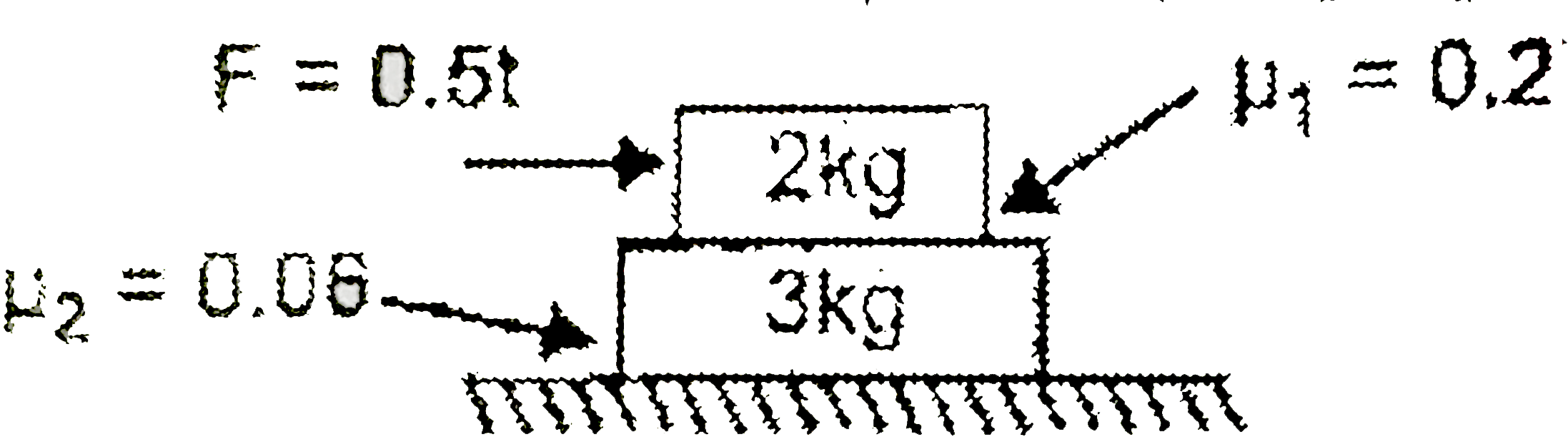
The acceleration time graph for 4 kg block is : Friction force acting between the two blocks at t=8 s
View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View Solution
