The amplitude and time period in SHM are 0.8 cm and 0.2 sec respectively. If the initial phase is π/2 radian, then the equation representing SHM is -
y=0.8cos10πt
y=0.8sinπt
y=3×0.8sinπt
y=0.8sin10πt
The correct Answer is:A
To find the equation representing Simple Harmonic Motion (SHM) given the amplitude, time period, and initial phase, we can follow these steps:
Step 1: Identify the given values
- Amplitude (A) = 0.8 cm
- Time period (T) = 0.2 sec
- Initial phase (Φ) = π/2 radian
Step 2: Write the general equation of SHM
The general equation for SHM can be expressed as:
y(t)=Asin(ωt+Φ)
where:
- y(t) is the displacement at time t
- A is the amplitude
- ω is the angular frequency
- Φ is the initial phase
Step 3: Calculate the angular frequency (ω)
The angular frequency ω is related to the time period T by the formula:
ω=2πT
Substituting the given time period:
ω=2π0.2=10πradians/second
Step 4: Substitute the values into the SHM equation
Now we can substitute the values of A, ω, and Φ into the general equation:
y(t)=0.8sin(10πt+π2)
Step 5: Simplify the equation using trigonometric identities
Using the trigonometric identity sin(π2+θ)=cos(θ), we can rewrite the equation:
y(t)=0.8cos(10πt)
Final Equation
Thus, the equation representing the SHM is:
y(t)=0.8cos(10πt)
- Amplitude (A) = 0.8 cm
- Time period (T) = 0.2 sec
- Initial phase (Φ) = π/2 radian
The general equation for SHM can be expressed as:
y(t)=Asin(ωt+Φ)
where:
- y(t) is the displacement at time t
- A is the amplitude
- ω is the angular frequency
- Φ is the initial phase
The angular frequency ω is related to the time period T by the formula:
ω=2πT
Substituting the given time period:
ω=2π0.2=10πradians/second
Now we can substitute the values of A, ω, and Φ into the general equation:
y(t)=0.8sin(10πt+π2)
Using the trigonometric identity sin(π2+θ)=cos(θ), we can rewrite the equation:
y(t)=0.8cos(10πt)
Thus, the equation representing the SHM is:
y(t)=0.8cos(10πt)
Similar Questions
The amplitude and the time period in a S.H.M. is 0.5 cm and 0.4 sec respectively. If the initial phase is π/2 radian, then the equation of S.H.M. will be
View SolutionThe amplitude and the periodic time of a S.H.M. are 5 cm and 6 sec respectively. At a distance of 2.5 cm away from the mean position, the phase will be
View Solution
Knowledge Check
Two particles execute SHM of same amplitude and same time period, about same mean position but with a phase difference between them. At an instant they are found to cross each other at x=+A3. The phase difference between them is
A2cos−1(15)B2sin−1(15)C2cos−1(13)D2sin−1(15)
The time period and the amplitude of a simple pendulum are 4 seconds and 0.20 meter respectively. If the displacement is 0.1 meter at time t=0, the equation on its displacement is represented by :-
View SolutionTwo linear SHM of equal amplitudes A and frequencies ω and 2ω are impressed on a particle along x and y−axes respectively. If the initial phase difference between them is π/2. Find the resultant path followed by the particle.
View SolutionThree sinusodal waves having amplitudes a, a/2 and a/3 are superposed. They have the same period and thelr phase are 0, π/2 and respectively. Find (i) The resultant amplitude and phase (ii) Draw a sketch to show the resultant wave.
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
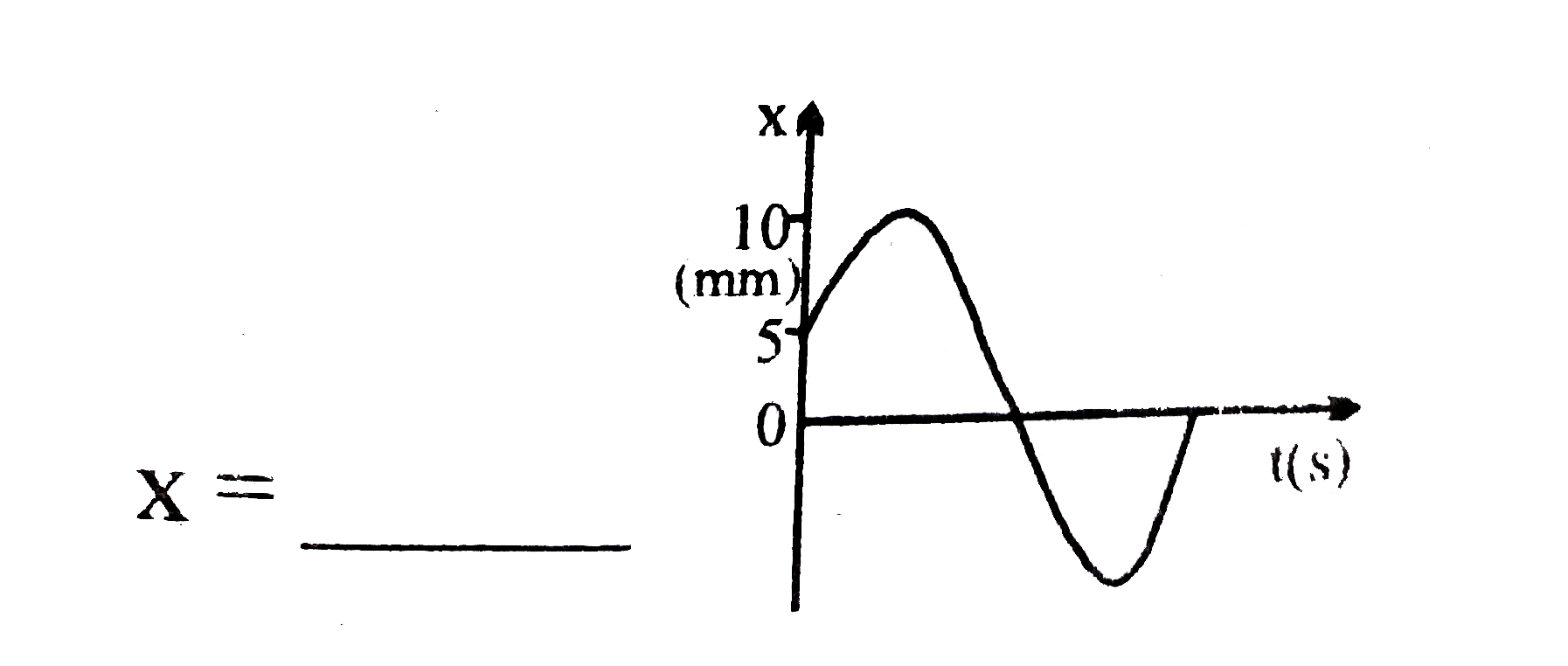
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
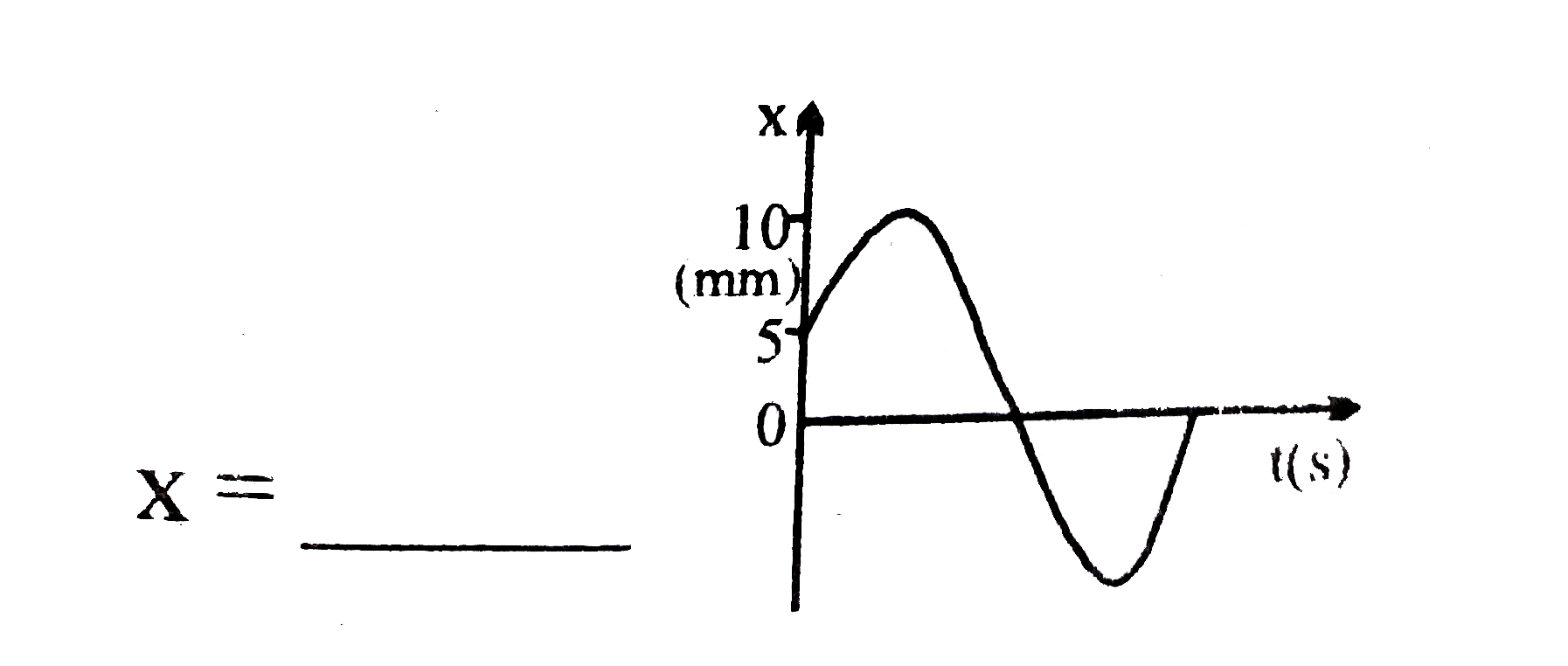
View SolutionTwo SHM's with same amplitude and time period, when acting together in perpendicular directions with a phase difference of π2 give rise to
View SolutionThe motion of a particle in S.H.M. is described by the displacement function, x=Acos(ωt+ϕ), If the initial (t=0) position of the particle is 1cm and its initial velocity is ωcms−1, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM:x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions ?
View Solution
